Én iPhone per menneske?

Det er nu mere end 10 år siden, at Steve Jobs præsenterede den første iPhone på en konference i Californien. Siden da er salget af den populære smartphone steget eksponentielt, og Apple har solgt mere end 1 milliard telefoner. 

 

Hvis denne udvikling fortsætter, hvornår vil der så være solgt ligeså mange iPhones, som der er mennesker i verden?

Ved en grov forsimpling antager vi, at antallet af solgte iPhones, tilnærmelsesvis følger en eksponentiel vækstfunktion. 
Vi vil altså gerne kunne beskrive salget ved følgende funktion:
\( I(t) = I_0\,\textrm{e}^{v\,t} \)
hvor I er antallet af iPhones til tiden t, og v er vækstraten. 

Nedenstende figur viser data over antallet af solgte iPhones samt en tilhørende regression.

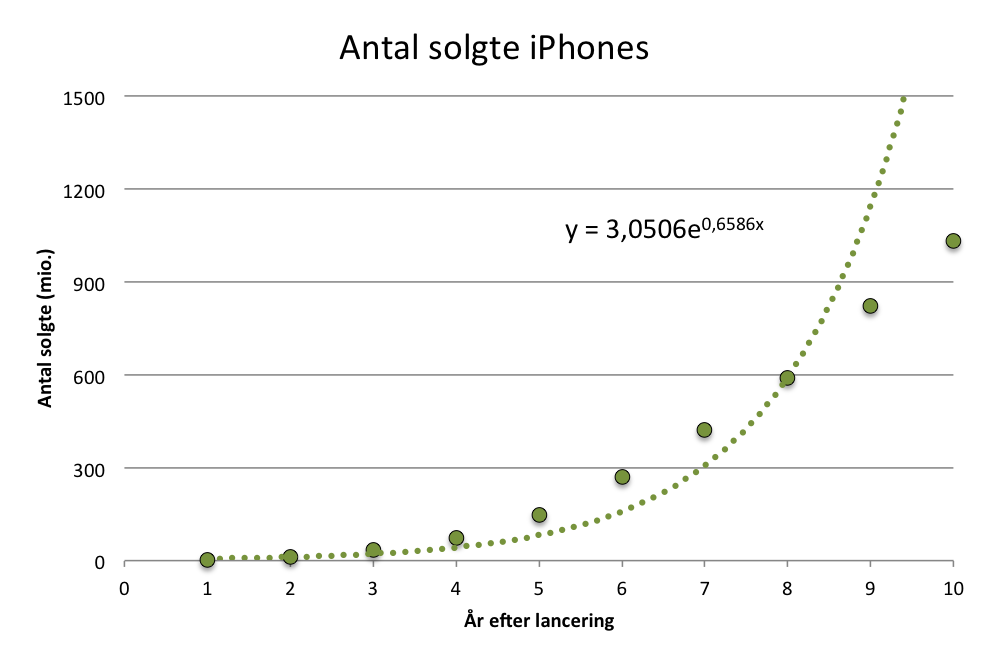
Antal solgte iPhones kan altså tilnærmelsesvist beskrives således: 
$$ I(t) = 3{,}0506\,\textrm{e}^{0{,}6586\,t} $$

Befolkningstilvækst

Samtidig med at salget af iPhones stiger, vokser verdens befolkning dog også. Vi kan altså ikke nøjes med blot at undersøge, hvornår vores funktion er lig med verdens nuværende befolkning. 

I stedet skal vi opstille et funktionsudtryk for befolkningstilvæksten på jorden og sætte de to funktioner lig med hinanden og løse for tiden.
Vi antager igen, at jordens befolkning følger en eksponentiel vækstfunktion:
$$ P(t) = P_0\,\textrm{e}^{r\,t} $$
Vi sætter vores startår til 2007 således at \(P_0\) angiver antal mennesker på jorden i 2007 og t angiver antal år derefter.

Ifølge verdensbanken var der i 2007, da den første iPhone udkom, 6.676mio. mennesker i på jorden og en befolkningstilvækst på 1.23%.
Vi har således, at \(P_0 = 6.676\) mio. og \(r = 0,0123\). Hvilket giver os følgende funktion:
$$ P(t) = 6.676\,\textrm{e}^{0{,}0123\,t} $$

Da vi nu både har en funktion for antal iPhones og antal mennesker på jorden kan vi nu bestemme for hvilken tid, t, de er lig med hinanden.

Dette gøres algebraisk, hvorefter vi kan indsætte de konkrete talværdier:

\( I_0\,\textrm{e}^{v\,t} = P_0\,\textrm{e}^{r\,t} \)

Vi tager logratimen på begge sider:
\( \log(I_0) + v\,t = \log(P_0)+v\,t \)

Isolerer:
\( \ln(I_0) - \ln(P_0) = v\,t-r\,t \)

\( \ln\left(\frac{I_0}{P_0}\right) = t\left(r - v\right) \)

Vi opnår altså:
\( \frac{\ln\left(\frac{I_0}{P_0}\right)}{r - v} = t \)

Nu kan vi så indsætte vores fundne talværdier:

\(\frac{\ln\left(\frac{3{,}0506}{6.676}\right)}{0{,}0123 - 0{,}6586} = 11{,}90 \textrm{år}\)

Det vil sige, at ifølge denne model vil andelen af iPhones overstige antallet af mennesker på jorden 11,91 år efter lanceringen af den første iPhone. Eller helt nøjagtigt den 28. maj 2019 kl. 05:03. Så hold godt øje den dag. 

 

 Alternativt

Der kan dog argumenteres for, at en eksponentiel funktion måske ikke er den bedste funktion til at beskrive salget af iPhones. Lad os i stedet forsøge med en potensfunktion.

 

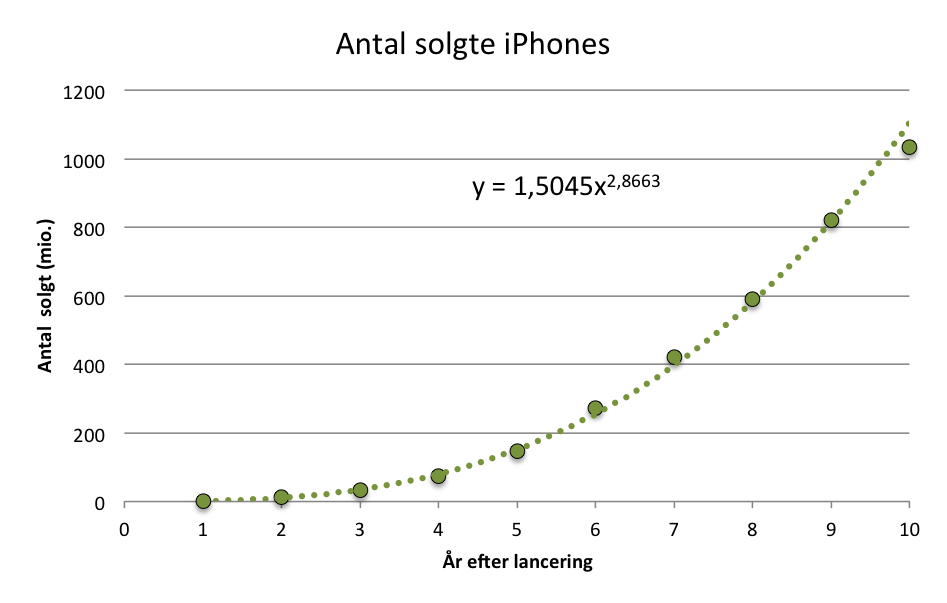
Her kan vi se, at der i højere grad er overensstemmelse mellem funktionen og regressionslinjen. Det er tilgengæld svært at løse denne funktion og funktionen for befolkningsstørrelsen algebraisk - men vi kan i stedet gøre det grafisk.

 

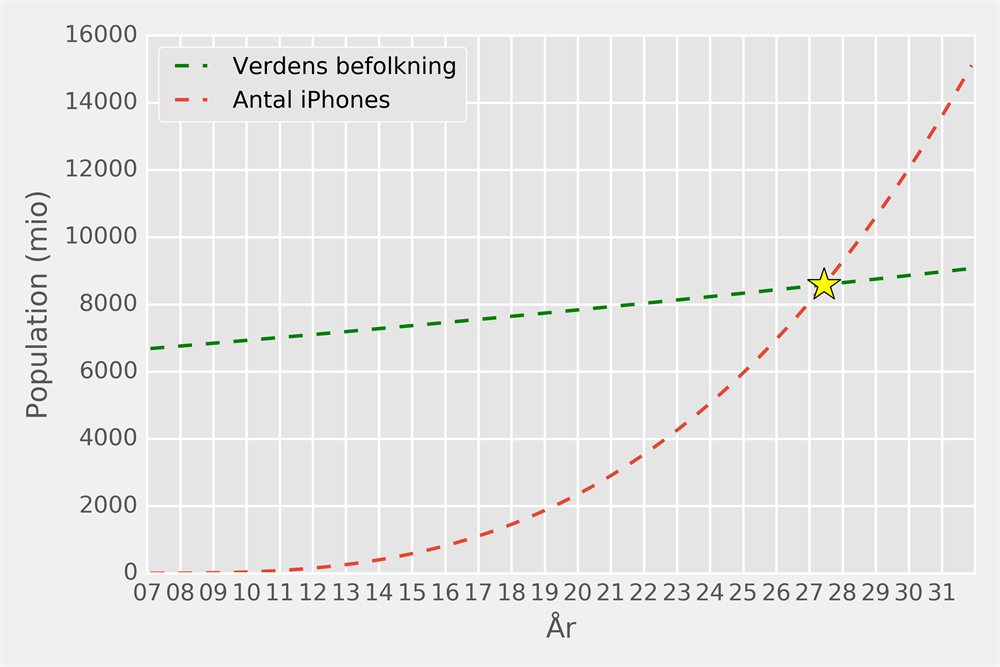
Ifølge denne model vil det altså først være i midten af 2027, at antallet af iPhones er det samme som antallet af mennesker. 

Forbehold:

Vi har gjort et par stærkt forsimplende antagelser angående befolkningstilvæksten og iPhonesalget. I begge tilfælde er der formentlig tale om logistisk vækst.

 

Kilder

http://data.worldbank.org/indicator/SP.POP.TOTL

http://data.worldbank.org/indicator/SP.POP.GROW 

https://www.statista.com/topics/847/apple/