Strandet hval
I tirsdags strandede en finhval ved Blokhus i Nordjylland. Finhvalen er den næststørste hvalart i verden, og de kan blive op til 27 meter lange og veje helt op mod 80 ton.

Den strandede hval er cirka 20 meter lang og vurderes til at være 30 ton (Kilde: TV2). Vi har undersøgt disse oplysninger og vurderer, at hvalen faktisk er en del tungere, nemlig 48,7 ton.
Finhvaler opholder sig normalt i grønlandsk farvand, men de kan svømme cirka lige så hurtigt, som Usain Bolt kan løbe, og det betyder, at en finhval kan svømme fra Grønland til Danmark på 29 dage - hvis den altså svømmer hele tiden.
Sådan har vi regnet det ud:
Massen af finhvalen
Ud fra billedet herunder kan vi estimere målene af en finhval.
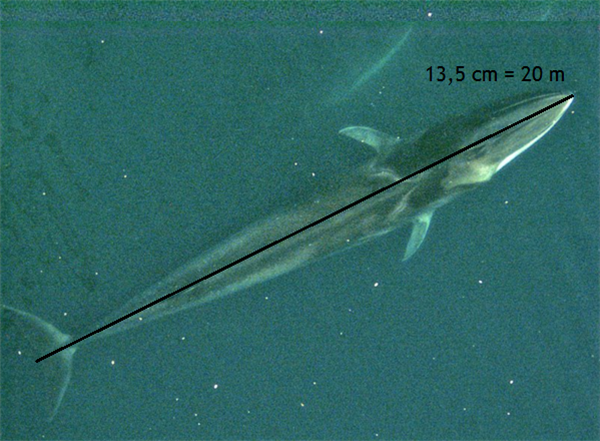
Ud fra billedet kan vi udregne målestoksforholdet: 13,5 cm svarer til 20m (2000 cm) - i virkeligheden. Målestoksforholdet udregnes ved først at forlænge brøken med 10, så vi ikke har decimaltal i brøken:
$$ \frac{13,5}{2.000} = \frac{135 }{20.000} $$
Herefter kan vi forkorte brøken med 5: $$\frac{135 }{20.000 } = \frac{27}{4000} $$
Det vil sige, at målestoksforholdet er 27:4000. Vi kan udregne, hvad 1 cm svarer til: $$\frac{4.000 \, \mathrm{cm \, pr. \,cm}}{27 \, \mathrm{cm}}=148 \, \mathrm{cm}$$
På billedet måles længden af hoved, hale og midten af kroppen. Herudover måles også diameteren to steder:
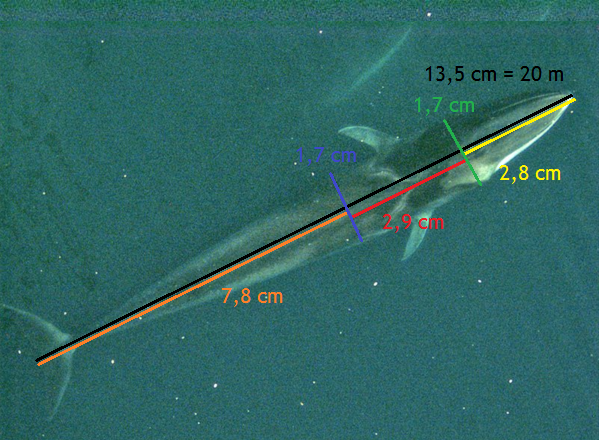
Vi estimerer, at hoved og hale kan ses som kegler og kroppen som en cylinder, fordi vi har målt de to diametre til at være lige store.
Vi udregner derfor længden af hoved, hale og midten af kroppen:
Halen er målt til 7,8 cm: \(7,8 \mathrm{cm} \cdot 148 \mathrm{cm \,pr. cm} = 1.154 \mathrm{cm} = 11,54 \mathrm{m}\)
Hovedet er målt til 2,8 cm: \(2,8 \mathrm{cm} \cdot 148 \mathrm{cm \, pr. cm} = 414 \mathrm{cm} = 4,14 \mathrm{m}\)
Kroppen er målt til 2,9 cm: \(2,9 \mathrm{cm} \cdot 148 \mathrm{cm \,pr. cm} = 429 \mathrm{cm} = 4,29 \mathrm{m}\)
Herudover skal vi også finde radius af hvalen. Diameteren måles til 1,7 cm, både ved halen, og radius vil derfor være \(0,5 \cdot 1,7 \mathrm{cm} = 0,85 \mathrm{cm}\)
Radius omregnes til meter på samme måde som de andre mål:
\(0,85 \mathrm{cm} \cdot 148 \mathrm{cm \, pr. cm} = 126 \mathrm{cm} = 1,26 \mathrm{m}\)
Nu skal vi bruge formlen for rumfang af en kegle:
$$V_{\mathrm{kegle}}=\frac{\pi\cdot h\cdot r^2}{3}$$
Nu er det muligt at udregne hovedets rumfang:
$$V_{\mathrm{hoved}}=\frac{\pi\cdot 4,14 \mathrm{m}\cdot (1,26 \mathrm{m})^2}{3} = 6,88\mathrm{m}^3$$
Herefter udregnes halens rumfang:
$$V_{\mathrm{hale}}=\frac{\pi\cdot 11,54 \mathrm{m}\cdot (1,26 \mathrm{m})^2}{3} = 19,19 \mathrm {m}^3$$
Herefter kan kroppens rumfang beregnes me formlen for rumfang af en cylinder:
$$V_{\mathrm{cylinder}}=h\cdot\pi\cdot r^2$$
$$V_{\mathrm{krop}}=4,29 \mathrm{m}\cdot\pi\cdot (1,26 \mathrm{m})^2=21,4 \mathrm{m}^3$$
Vi udregner hvalens samlede volumen:
$$6,88\mathrm{m}^3 + 19,19 \mathrm {m}^3 + 21,4 \mathrm{m}^3 = 47,47 \mathrm{m}^3$$
Formlen for udregning af massefylde er \( \rho = \frac{m}{V}\), og denne formel kan omskrives til \( m = \rho\cdot V\)
Vi regner med, at massefylden af en finhval er på størrelse med massefylden for en blåhval, der er på 1025 kg/m3. Vi udregner massen af finhvalen:
$$m = 1025 \mathrm{kg/m}^3 \cdot 47,47 \mathrm{m}^3 = 48.652 \mathrm{kg} $$
Hvalen vejer altså i følge modellen 48,7 ton og ikke kun 30 ton.
Hvalens svømmehastighed
Afstanden mellem Danmark og Grønland er cirka 2800 km. En finhval kan svømme 40 km/t - hurtigere end Usain Bolt i gennemsnit løber, når han løber 100-meter.
Herudfra kan vi udregne, hvor lang tid det tager for en finhval at svømme til Grønland:
$$\mathrm{afstand} = \mathrm{hastighed} \cdot \mathrm{tid}$$
$$\frac{\mathrm{afstand}}{\mathrm{hastighed}}= \mathrm{tid}$$
Først omregnes 40 km/t til enheden m/s: 40 km = 40.000 m, og 1 time er 3600 sekunder, da \(60 \mathrm{sek/min.} \cdot 60 \mathrm{min./t} = 3600 \mathrm{s/t}\)
$$40.000\mathrm{m}/3600 \mathrm{s} = 11,11 \mathrm{m/s}$$
$$\frac{28.000.000\mathrm{m}}{11,11\mathrm{m/s}}= 2.520.252 \mathrm{s}$$
Vi omregner til timer ved at dividere med 3600s/t:
$$\frac{2.520.252 \mathrm{s}}{3600 \mathrm{s/t}} = 700 \mathrm{t}$$

En finhval kan altså svømme til Danmark fra Grønland på 700 t, dvs. lidt under en måned: \(\frac{700\mathrm{t}}{24 \mathrm{t/døgn}}= 29,2 \mathrm{døgn}\)
Kilder:
https://da.wikipedia.org/wiki/Massefylde
https://en.wikipedia.org/wiki/Usain_Bolt#Average_speed
http://naturporten.dk/temaer/gr%C3%B8nlands-dyr/havpattedyr-gr%C3%B8nland/item/finhval-2
http://nyheder.tv2.dk/samfund/2016-02-23-hval-strandet-paa-nordjysk-strand-kan-vaere-kollideret-med-skib
Woodward et al. (2006): Morphological specializations of baleen whales associated with hydrodynamic performance and egological niche. Journal of Morphology.
tent
