Facebook-likes

Matematikcenters facebookside har rundet 4000 likes, og vi rigtig glade for, at så mange mennesker støtter op om gratis matematikhjælp for alle!

Det er vores mål at nå 4500 fans inden udgangen af året. Herunder kan man se, antallet af likes har udviklet sig siden september 2013, hvor vi havde 3000 likes.

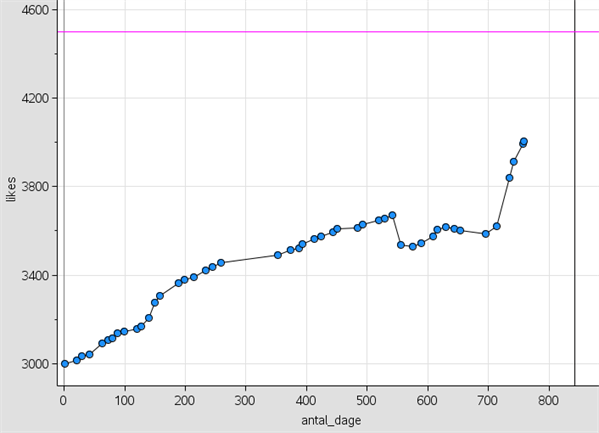
Den lodrette streg markerer slutningen af 2015, mens den vandrette lyserøde streg markerer målet, de 4500 likes. 

Vi vurderer, at antallet af likes over en længere periode vil udvikle sig efter den logistiske vækstmodel, hvorfor vi kan forvente, at udviklingen til at starte med vil være eksponentiel. Når vi laver logistisk regression, får vi en maksimalværdi for antallet af likes på 3899, og derfor kan denne model ikke passe. Denne forkerte værdi gives, fordi antallet af likes falder i foråret, hvor inaktive facebook-konti slettes. Derfor laver vi eksponentiel regression i stedet, fordi logisitisk vækst i starten er eksponentielt voksende. Når vi laver eksponentiel regression på vores data, får vi følgende graf: 

 

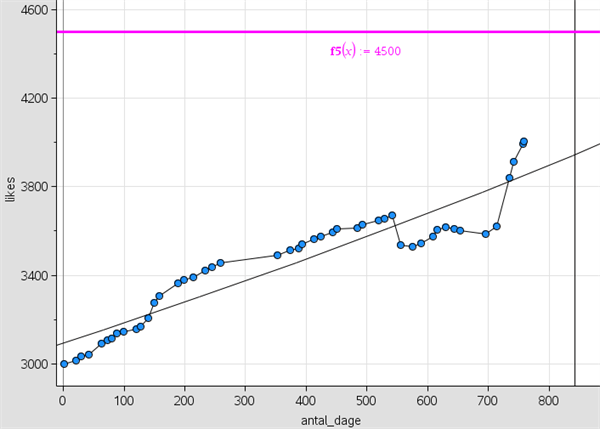
Som vi kan se, når vi ikke målet i følge modellen, og derfor har vi brug for vores følgere for at komme ud til flere. 

De sidste 11 #DerErMatematikiAlt-opslag fra Matematikcenter er nået ud til gennemsnitligt 1236 mennesker. Hvis opslaget i dag den 8. oktober 2015 når ud til lige så mange mennesker, og alle, der ser det, foreslår 3 venner at synes godt om Matematikcenter, vil 3708 personer blive inviteret:

$$3 \cdot 1236 = 3708$$

Vi udregner, hvor stor en del af disse personer, der skal like Matematikcenters side, før vi når de 500 likes, vi mangler: 

$$ \frac{3708 \mathrm{personer}}{500 \mathrm{likes}} =  7,4 \mathrm{personer/like} $$

Det vil sige, at der skal komme et like for hver 7,4 person, så hvis hver 7. liker Matematikcenter på facebook, vil målet være nået!