Ringridning

Igen i år holdes en stor ringridderfest i Sønderborg, hvor 500 heste og ryttere dyster om at blive ridderkonge eller -dronning. Måske der var mange der troede det, men ringridning er langt fra en død sport.

I ringridning skal du, på en galopperende hest, ramme din lansespids ind i en lille ring. Den største ring er 22 milimeter i diameter, men skiftes ud med mindre og mindre ringe i løbet af konkurrencen. Lansens længde kan varriere mellem 50 og 160 cm.

Hvor svært kan det være?

Eftersom ringen højest er 22 mm i diameter og det er den nemmeste ring at ramme, er det denne værdi vi regner på. Vi benytter gennemsnitslængden for lanser, svarende til 105 cm og regner ud, hvor meget man egentlig kan ryste på hænderne før man rammer ved siden af.

Man vil altid sigte efter at få lansespidsen ind i centrum af ringen, da det er den sikreste sejr. Fra centrum og ud til ringens kant er der 11 mm (eftersom ringen er 22 mm i diameter). Den længde danner sammen med lansens længde på 1050 mm og den yderste position lansen kan have for at ramme inde i ringen (den røde streg) en retvinklet trekant. 

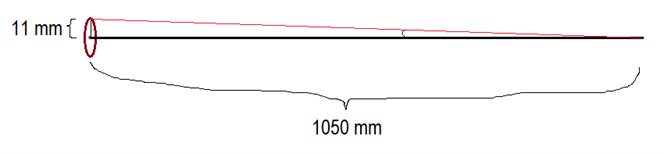
Ved hjælp af tangens kan man da beregne vinklen mellem lansens optimale position (sort) og dens yderposition.

$$tan^{-1}(\frac{11\text{ mm}}{1050\text{ mm}})=0,0105\text{ grader}$$

Lansens vinkel kan altså kun varriere 0,01 grader fra den optimale position! Det kræver altså en vis præcision at være dygtig til ringridning.

Sådan beregnede vi den gennemsnitlige lanse:

$$50\cdot 160=210$$

$$\frac{210\text{ cm}}{2}=105\text{ cm}=1050\text{ mm}$$