Logistisk vækst
En logistisk vækst er kendetegnet ved, at der er tale om en begrænset vækst. Der er altså et maksimum for, hvor funktionen kan vokse til. I starten vokser den med noget, der minder om en eksponentiel udvikling, men når den så nærmer sig sit maksimum, flader den ud.
Logistisk vækst bruges til at lave modeller over eksempelvis dyreverdenen. Hvis man sætter 10 kaniner ud på en ø, vil de til at starte med formere sig utroligt meget (høj væksthastighed). Når antallet af kaniner når en vis størrelse, vil øen ikke længere have mad nok til at brødføde alle kaninerne, og derfor vil væksthastigheden stilne af (kurven bliver fladere).
Differentialligningen
Logistisk vækst udtrykkes med differentialligningen
y′=y(b−ay)
Bemærk, at hvis man ganger parentesen ud, så får man en andengradsligning.
y′=b⋅y−a⋅y2
Eksempler på denne type differentialligning er
y′=y(5−2y),y′=10y−3y2,dydx=y⋅(4−4y).
Løsningen på ligningen er
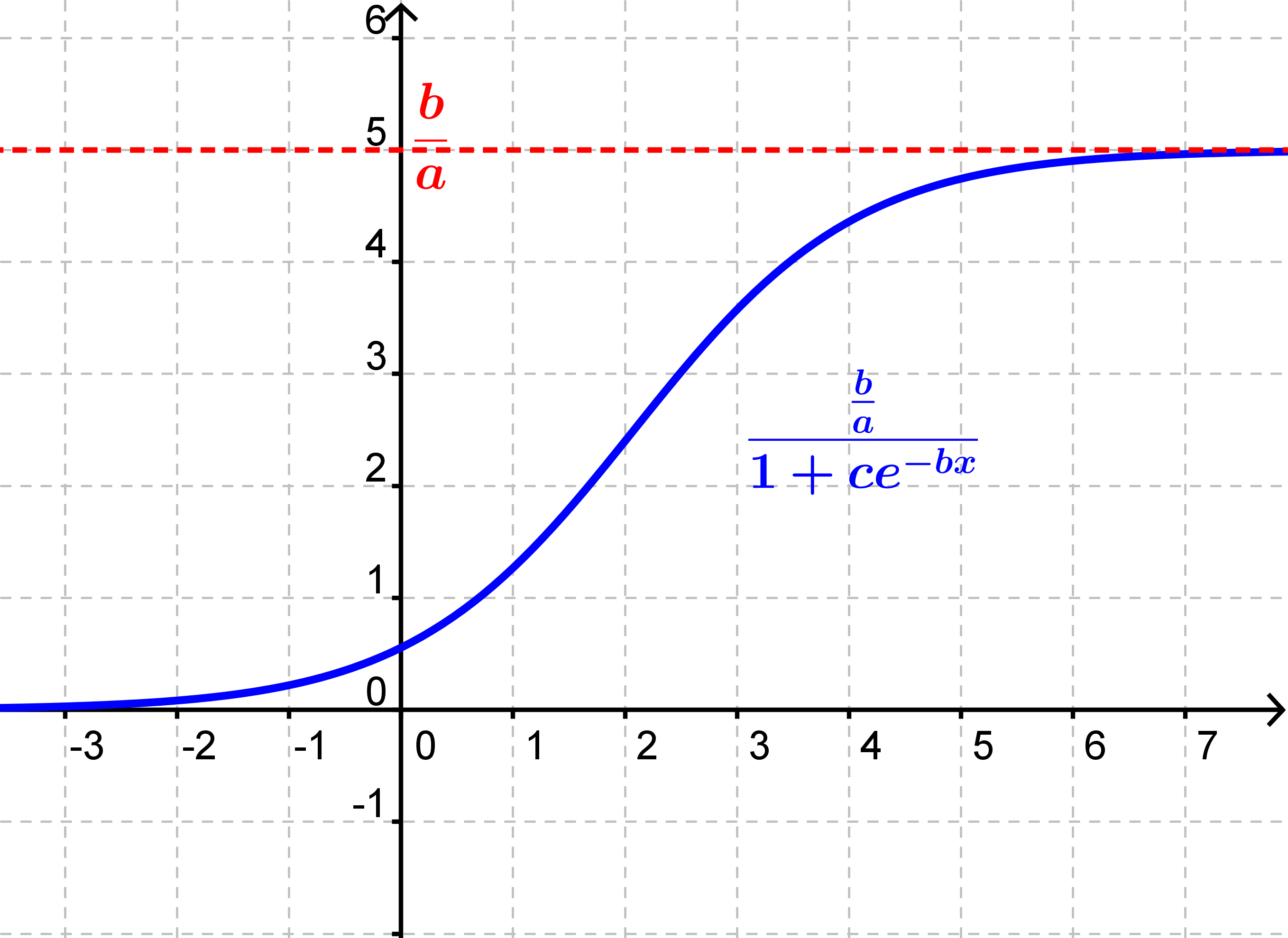
y=f(x)=ba1+ce−b⋅x
Eksempel
Hvis vores differentialligning er
y′=y⋅(10−5y)
så er løsningen
y=f(x)=1051+ce−10x=21+ce−10x
Når x vokser, vil eksponentialfunktionen i nævneren nærme sig 0. Dermed vil hele nævneren nærme sig 1, og brøken vil dermed være lig med tælleren b/a. Funktionerne vil altså vokse noget nært eksponentielt i starten men så flade ud og nærme sig b/a.
Nært beslægtet differentialligning
I differentialligningen ovenfor, så vi at løsningerne ville smyge sig op ad b/a. Dette kaldes populationens "steady state", og beskriver den øvre grænse for populationen.
Tit kender man "steady state", og derfor ville det være smart, hvis man kunne indsætte/aflæse det direkte i differentialligningen.
Hvis vi kalder "steady state" for M, så har vi, at:
M=ba⇔b=a⋅M
Hvis vi indsætter det i differentialligningen ovenfor, får vi
y′=y⋅(aM−ay)=ay⋅(M−y)
og løsningen bliver
y=f(x)=M1+ce−aMx
Egentlig er der tale om den samme differentialligning som før, men hvor vi bare kan aflæse M i stedet for b ud fra differentialligningen.
Uddybende forklaring til løsningen
Løsning af den logistiske differentialligning: y' = y(b-a y):
y′=dydx=y(b−ay)⇔dyy(b−ay)=dx;
der integreres på begge side og integrations konstanten adderes
∫1y(b−ay)dy=x+c
Brøken adskilles i to brøker, det antages at
1y(b−ay)=Ay+Bb−ay=A(b−ay)+Byy(b−ay)
Tælleren skal jo blive 1 og dermed A(b−ay)+By=1.
Dette giver to ligninger Ab=1 og −aAy+By=0 hvoraf A=1b og −aA+B=0⇔B=aA=ab.
Det vil sige
∫1y(b−ay)dy=∫1bydy+∫ab(b−ay)dy=log(y)b−∫1b(b−ay)d(b−ay)=log(y)b−log(b−ay)b=log(yb−ay)b=x+c
Eksponential funktionen tages på begge sider yb−ay=Exp(bx+bc) fra dette udtryk isoleres y
y=bexp(bx+bc)1+aexp(bx+bc)=b/a1+Cexp(−bx) hvor den nye integrations konstant er C.
( C=exp(−bc)/a )
