Olympiske lege
Nu er de Olympiske Lege godt i gang, og de har budt på medaljer af både guld, sølv og bronze til Danmark. Vi har set lidt nærmere på, hvordan man kan bruge matematikken til at analysere forskellige dele af sportens verden.

Vi ser på, hvorfor kuglestødere sender kuglen afsted med en vinkel på 37-38\(^\circ\), hvordan man sikrer en retfærdig start i fx 100-meterløb, og hvorfor man ikke kigger på 1000-dele, når svømmediciplinerne er uafgjort.
Den perfekte vinkel i kuglestød
I kuglestød skal atleten støde en kugle længst muligt. Mændenes kugle vejer over 7 kg, mens kvindernes vejer 4 kg.
Normalt når vi arbejder med det skrå kast er længden i \(x\)-retningen givet ved følgende formel:
$$\mathrm{x_{længde}}=\frac{v_0^2}{g}\cdot \sin(2\alpha)$$
Her er \(v_0\) starthastigheden, \(g\) tyngdeaccelerationen og \(\alpha\) er vinklen mellem jorden og den retning, som hastigheden \(v_0\) foregår i.
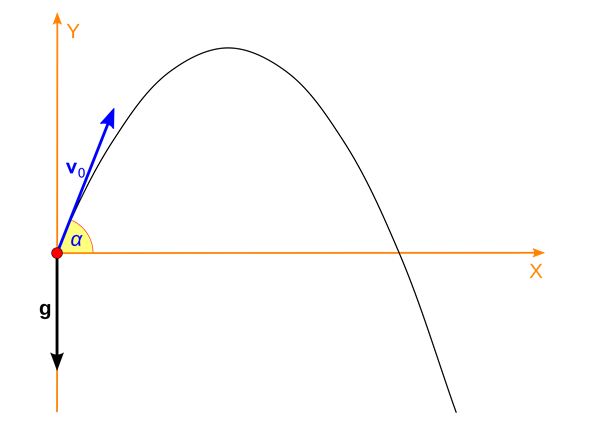
For at finde den vinkel, der giver det længste kast, kan vi differentiere funktionen mht. \(\alpha\) og løse f'(\(\alpha)\)=0:
f'(\(\alpha\))=\(\frac{v_0^2}{g}\cdot 2\cdot \cos (2\alpha)\)
\(0=\frac{v_0^2}{g}\cdot 2\cdot \cos (2\alpha)\)
Vi forudsætter, at hastigheden ikke er lig med 0 m/s (\(v_0\neq0\)), og derfor kan vi udlede, at \(\cos(2\alpha)=0\). Vi løser denne ligning ved at tage den inverse cosinus på begge sider:
$$\cos^{-1}(0)=2\alpha=90$$
$$\alpha=45$$
Vi kan altså konkludere, at det normalt er smartest at kaste med en vinkel på 45\(^\circ\). Men hvorfor støder kuglestødere så oftest med vinkler på helt ned til 37-38\(^\circ\)?
Dette mysterium har fået flere forskere til at kigge nærmere på biomekanikken bag kuglestød. Lenz og Rappl har skrevet artiklen "The optimal angle of Release in Shot Put" i 2010. Her beskriver de, at hvis man tager den højde, hvor atleten slipper kuglen, med i betragtning, falder den optimale vinkel til cirka 42\(^\circ\). Det skyldes, at kasteparablen ikke er symmetrisk omkring toppunktet, da kuglens bane starter højere oppe, end den slutter (se ovenstående illustration).
Derfor vil det være favorabelt for høje atleter at støde mere vandret, da de allerede slipper kuglen højt oppe i luften og derfor bør tilføje mere energi i \(x\)-retningen end i \(y\)-retningen. Hvor lille vinklen skal være, for at det er optimalt, afhænger af \(v_0\). Hvis man slipper kuglen i en højde af 2,15 m og sender den af sted med en starthastighed på 13,7 m/s, giver det en optimal vinkel på 42\(^\circ\).
Efter denne analyse, hvor man er kommet lidt tættere på de 37-38\(^\circ\), ser forskerne på luftmodstanden, som de konkluderer ikke har nogen større betydning.
Hvad der derimod kan forklare, at den optimale vinkel er mellem 37 og 38\(^\circ\) og ikke 42\(^\circ\) er tyngdekraften på kuglen og den kraft, som atleten kan udøve på kuglen ved forskellige vinkler. Det er svært at kvantisere atletens styrke ved forskellige vinkler, men man kan se, at verdensrekorden i bænkpres (335 kg) (til venstre på figuren herunder) er noget højere end verdensrekorden i stød ("clean and jerk") (263 kg), der ses til højre på figuren herunder.
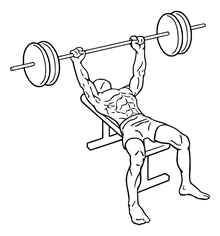
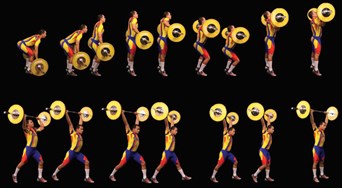
Det tyder på, at mennesket er bedre til at udøve en kraft med armene vinkelret væk fra kroppen end med armene over hovedet. Det medvirker til at det er mere favorabelt at have en mindre vinkel i kuglestød, da kuglestøderen kan lægge mere kraft i kuglen, hvis den bliver stødt mere fladt.
Vi kan også se på tyngdekraftens påvirkning:
Energien, som kuglen har, kan deles op i kinetisk og potentiel energi: \(E_{total}=E_{kin}+E_{pot} = \frac{1}{2}mv_0^2+mg\delta h\)
Her er \(\delta h\) forskellen mellem håndhøjde og skulderhøjde, når kuglen slippes.
Ud fra dette udtryk kan vi se, at jo højere kuglen bliver stødt, jo lavere bliver initialhastigheden, når \(E_{total}\) er konstant. Da den optimale vinkel afhænger af \(v_0^2\) (og ikke bare \(v_0\), vil dette altså have stor betydning for maksimallængden i x-retningen, og det vil derfor være favorabelt med lavere vinkler, der giver mindre højde. Det kan altså betale sig at satse på den kinetiske energi i stedet for den potentielle energi.
Alt dette medfører, at det er mest favorabelt at støde kuglen med en mindre vinkel end de normale 45\(^\circ\).
Startskud i 100 m-løb
Til store stævner som OL bruger man ikke længere en traditionel startpistol med krudt.
I stedet bruger man en elektrisk pistol, en "silent gun", der ikke selv siger nogen lyd, men i stedet sender signal til 8 højttalere, der er placeret bag hver løber på startblokken.
Hvis startskuddet skydes af inde fra græsset i midten af stadion, vil det nemlig tage længere tid for lyden af nå løberen på den yderste bane (bane 8). Ved at hver løber har deres egen højttaler, kan de høre signalet på præcist samme tid. Lad os se på, hvad det ville betyde, hvis man ikke brugte "silent guns":
Vi antager, at starteren, der affyrer skuddet, står ved startstregen tre meter inde på græsset i midten af stadion. En løbebane er 1,22 m bred, og vi antager, at atleterne er placeret i midten af banen, dvs. \(0,5\cdot 1,22\,\mathrm{m}=0,61\, \mathrm{m}\) inde hver bane. Den første atlet er altså 3 m+0,61 m = 3,61 m væk fra starteren. Vi regner ud, hvor langt den sidste atlet på bane 8 er fra starteren: \(3 \, \mathrm{m}+7\cdot 1,22\, \mathrm{m}+0,61 \, \mathrm{m}= 12,15 \, \mathrm{m}\)
Der er altså 12,15 m - 3,61 m = 8,54 m mellem de to atleter.
Lyden bevæger sig med 343 meter i sekundet. Vi udregner, hvor lang tid det tager for lyden at bevæge sig 8,54 meter:
$$\frac{8,54 \, \mathrm{m}}{343 \, \mathrm{m/s}}=0,0249 \, \mathrm{s}$$
Det betyder, at atleten på inderste bane får et forspring på 0,0249 sekunder - og det er meget i forhold til verdensrekorden på 100 m.
Hvis man stadig brugte traditionelle pistoler, ville det derfor være mere lige for atleterne, hvis de kiggede efter røgen fra pistolen, da lyset bevæger sig med hele \(3 \cdot 10^8\) m/s. Når der er 8,54 m mellem løberen på bane 1 og bane 8, betyder det altså kun en forsinkelse på \(\frac{8,54\, \mathrm{m}}{3\cdot 10^8 \, \mathrm{m/s}}=2,85 \cdot 10^{-8}\, \mathrm{s}\). Det er ikke en forskel, som kan ses på resultattavlen, men det ville formentlig være uhensigtsmæssigt for løberne at skulle kigge til siden og reagere på røgen i stedet for at kigge fokuseret ned i jorden og vente på lyden.
Hvorfor bruges 1000-dele ikke i svømning?
Sammenlignet med andre sportsgrene er der rigtig ofte uafgjorte resultater i svømning. Eksempelvis blev dette OL's finale i 100 m butterfly vundet af J. Schooling, mens andenpladsen blev delt af hele tre svømmere, nemlig M. Phelps, C. Le Clos og L. Sceh. Svømning afgøres på 100-dele af et sekund, men de tidstagningsmetoder, der er tilgængelige, kan sagtens give meget mere præcise resultater. Så hvordan kan det egentlig være, at man ikke kigger på 1000-dele, når et løb er endt uafgjort?
Lad os først se lidt på, hvor hurtigt man kan svømme 50 m (50.000 mm).
Den hurtigste svømmestil er freestyle (crawl), hvor mændenes verdensrekord er 20,91 s på langbane (som også bruges til OL). Vi udregner, hvor langt man med denne gennemsnitsfart kan svømme på en tusindedel af et sekund:
$$\frac{50.000 \,\mathrm{mm}}{\frac{20,91\, \mathrm{s}}{0,001\, \mathrm{s}}}=2,39 \, \mathrm{mm}$$
2,39 mm er ikke meget, når man tager målene for bassinet med i overvejelserne: FINA (svømmeforbundenes verdensorganisation) tillader, at poolen er op til 3 cm for lang, fordi det er svært at bygge pools, der er præcist 50 m lange. Hvis man gik ind og kiggede på tusindedele, ville man ikke kunne være sikker på, at en atlet, der svømmede 3/1000-dele hurtigere end konkurrenten, ikke bare havde en bane, der var \(3\cdot 2,39\,\mathrm{mm}=7,17\,\mathrm{mm}\) kortere.
Derfor vælger man at lade løbet være uafgjort i stedet.
Kilder:
https://www.technologyreview.com/s/420079/biomechanical-problem-of-shot-putting-finally-solved/
http://arxiv.org/pdf/1007.3689v2.pdf
http://www.psfk.com/2012/08/silent-track-and-field-pistol.html
http://denstoredanske.dk/Livsstil,_sport_og_fritid/Sport/Atletik/atletik
http://condellpark.com/kd/reactiontime.htm#erp
https://en.wikipedia.org/wiki/World_record_progression_50_metres_freestyle
http://regressing.deadspin.com/this-is-why-there-are-so-many-ties-in-swimming-1785234795
http://www.fina.org/sites/default/files/rules-print-pdf/8458.pdf
https://en.wikipedia.org/wiki/Progression_of_the_bench_press_world_record
https://en.wikipedia.org/wiki/Clean_and_jerk#World_records
