Dome of Visions
Ved Den sorte Diamant i København står Dome of Visions, der er et eksperiment inden for bæredygtigt byggeri. NCC står bag bygningen, der normalt er fyldt med events, udstillinger og koncerter.

Man ikke skal kaste med sten, hvis man bor i et glashus, og selvom Dome of Visions' facade er lavet af hårdt plast, gør det samme sig nok gældende her. Dome of Visions er 10,5 m høj, og det betyder, at rumfanget er på cirka 2400 kubikmeter. Det betyder, at der kan være over 2,47 milliarder småsten i Dome of Visions, hvis hver sten har samme størrelse og form som en M&M's!
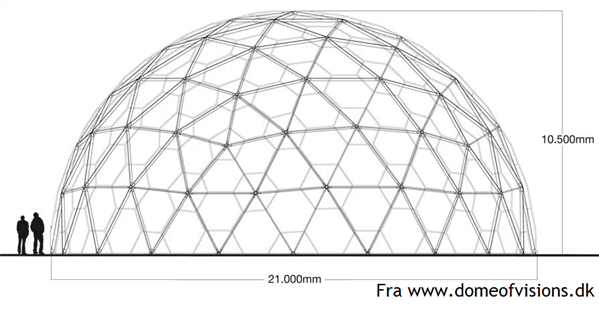
Sådan har vi regnet det ud:
Geodætiske kupler er bygget ud fra det, som man kalder de platoniske legemer – det er figurer, der er opbygget af en slags (lige store) flader sat sammen i kanterne – eksempelvis er den sekskantede terning sat sammen af firkanter og derfor et platonisk legeme.
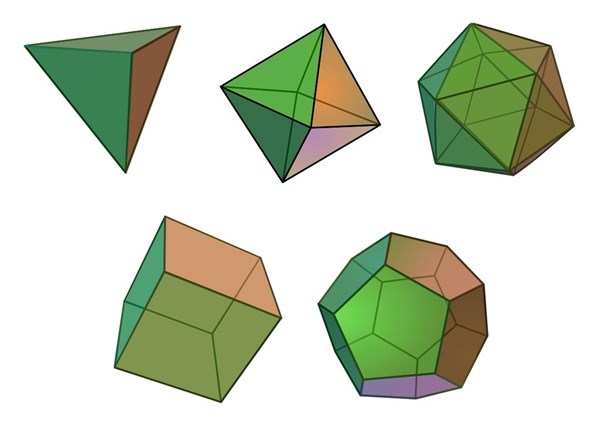
Geodætiske kupler er tit lavet ud fra isokaederen – et legeme sat sammen af 20 trekanter - figuren øvert til højre herover. En kuppel svarer altså til en halv isokaeder.
Når man skal bygge en bygning, er man ofte interesseret i at få så stor et rumfang som muligt, samtidig med at man vil spare på materialerne. På den måde vil man få mest bygning for pengene. Den geometriske struktur, der har det største rumfang set i forhold til overfladearealet, er kuglen.

Derfor vil vi gerne have vores kuppel til at være mere rund, så den får et større rumfang. Det gør vi ved at dele hver trekant i den halve isokaeder op i flere små trekanter. Hvis vi deler hver trekants side op i 2, får vi en såkaldt 2v kuppel. Deler vi den op i 3, får vi en 3v kuppel og så videre. Jo flere trekanter, en dome består af, jo mere vil den ligne en kugle.
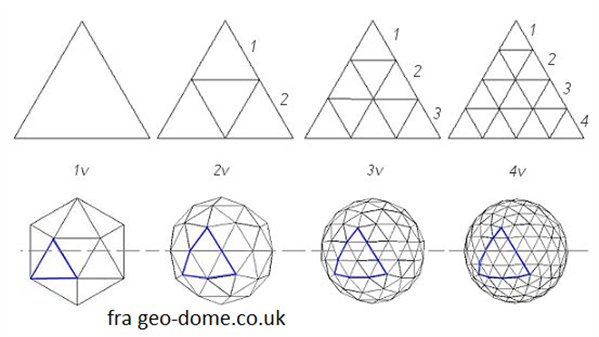
Dome of Visions er en 4v-dome, der er 10,5 m høj. Det er indviklet at regne rumfanget af domer, fordi de små trekanter alle sammen buler lidt ud for at give domen en overflade, der er så rund som muligt.
Det gør, at vinkler og længder ændres lidt, så figuren bliver sværere at regne på.
Fordi Dome of Visions er en v4-dome, er den ret tæt på at være en halvkugle.
En halvkugle af med samme radius har et volumen på
$$V = \frac{\frac{4}{3} \cdot\pi \cdot r^3}{2}$$
$$V = \frac{\frac{4}{3} \cdot\pi \cdot 10,5^3}{2} = 2424,5 m^3$$
Sten i et plasthus
Dome of Visions er normalt fyldt med udstillinger, koncerter, events og lignende. Men hvis vi nu i stedet fyldte plasthuset op med småsten, der havde samme form og størrelse som M&M’s – hvor mange ville der så kunne være?
En gruppe matematikere har undersøgt, hvordan de små chokoladeknapper fordeler sige i en æske, der har en kvadratisk bund. De nåede frem til, at 66,5 % af beholderen blev fyldt af M&M’s, mens de resterende 33,5 % af æskens indhold er luft, der ligger imellem chokoladeknapperne. Vi forudsætter, at vores småsten fordeler sig på samme måde i Dome of Visions. Vi udregner, hvor meget 66,5% af de 2424,5 kubikmeter er, for at finde ud af, hvor mange kubikmeter, der vi blive optaget af småstenene. Herefter omregnes til liter ud fra, at der går 1000 L på 1 kubikmeter:
$$ \frac{2424,5 m^3}{100\%}\cdot 66,5 \% = 1.612,3 m^3 = 1.612,29 m^3 \cdot 1000 L/m^3 = 1.612.290 L $$
Der kan altså være over 1,6 millioner L småsten i Dome of Visions.
M&M's (og i dette tilfælde vores småsten) er et specialtilfælde af ellipsoider.
Ellipsoider har et volumen, der kan beregnes ud fra følgende formel: $$V_{\text{ellipsoide}} = \frac{4}{3}\pi\cdot \text{a}^2\cdot \text{b}$$
Her er a radius for en M&M, og b er halvdelen af højden, hvor en M&M er tykkest. a = 0,67 cm og b = 0,3465 cm for en almindelig M&M.
Vi udregner, hvad volumen af en M&M’s er:
$$ V = \frac{4}{3}\pi\cdot 0,67^2 cm \cdot 0,3465 cm = 0,651541 \text{cm}^3 $$
Vi omregner rumfanget til liter ud fra, at der er 1000 kubikcentimeter på en liter: $$\frac{0,651541 cm^3}{1000 cm^3/L} = 0,000651541 L$$
Vi udregner antallet af småsten, der går på 1.612.290 L: $$ \frac{1.612.290 L }{0,000651541 L / \text{småsten}} = 2.474.579.496,9 \text{småsten} $$
Der kan altså være mere end 2,47 milliarder småsten i Dome of Visions.

Kilder:
http://ing.dk/artikel/en-matematisk-analyse-af-slikposer-60670
http://www.plunk.org/~grantham/public/geodesic_domes/geodesic_domes.html
http://www.elab-hackerspace.org/2015/09/08/geodesic-dome/
