Appelsiner på Smukfest - Banach-Tarski-paradokset

I denne uge bliver Smukfest afholdt under bøgetræerne ved Skanderborg. Her samles festglade mennesker til hygge og god musik i naturen.

I løbet af festivallen bliver der spist og ikke mindst drukket rigtig meget. På Smukfest kan man få vodka/juice-drinks lavet på friskpressede appelsiner i de kendte appelsinboder.

Smukfest oplyser, at de sidste år brugte 126.700 kg appelsiner i appelsinboderne. Det er selvsagt rigtig mange appelsiner. Hvis en gennemsnitlig appelsin vejer 131 g, bliver der brugt 976.176 appelsiner til Smukfest. Hvordan får man fat i så mange appelsiner? Her kan matematikken hjælpe!

Ved hjælp af Banach-Tarskis paradoksale teorem kan Smukfest nemlig nøjes med at købe én enkelt appelsin og alligevel ende med at have appelsiner nok - i hvert fald teoretisk set.

Sådan fungerer det

Uendeligheder

For at man kan forstå Banach-Tarskis paradoks, skal man først se lidt på uendeligheder. En type uendelighed er tællelige uendeligheder. Et eksempel på en tællelig uendelighed er de naturlige tal - altså de tal, vi normalt tæller med. Den mængde af tal defineres på denne måde:

$$\mathbb{N}=\{1,2,3,4,5,...,n,n+1,...\}$$

Mængden er uendeligt stor, og vi vil altid kunne gå fra ét tal i mængden til et andet tal i mængden i et endeligt (tælleligt) antal skridt. Eksempelvis kan vi gå fra 1 til 5 via 2, 3 og 4. Derfor kaldes mængden en tællelig uendelighed.

En utællelig uendelighed er eksempelvis alle de reelle tal mellem 0 og 1. Man kan simpelthen ikke gå fra 0 til 1 i et endeligt (tælleligt) antal skridt, hvor alle tal mellem 0 og 1 indgår. 

Lad os nu se på mængden af lige tal og mængden af ulige tal:

\(\{2,4,6,8,10,...\}\) og \(\{1,3,5,7,9,...\}\)

Man kunne umiddelbart tro, at der er halvt så mange lige tal, som der er naturlige tal - og på samme måde at der er halvt så mange ulige tal, som der er naturlige tal. Det er bare ikke tilfældet. Der er altså uendeligt mange lige tal og uendeligt mange ulige tal.

For hvert naturligt tal kan man altid finde fx et lige tal:

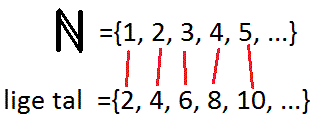
Ved at dele de naturlige tal op i lige og ulige tal kan man altså skabe to tællelige uendeligheder ud fra én tællelig uendelighed! At man kan skabe to uendelige sæt ud fra ét oprindeligt uendeligt sæt (hvor alle sæt har samme størrelse) er en del af fundamentet for beviset for Banach-Tarski-paradokset. Her vil vi ikke se på hele beviset, men bare på konceptet i det.

Den matematiske sfære

Men hvad har det med appelsiner og Smukfest at gøre? En hel del, faktisk, hvis man ser appelsiner som matematiske sfærer. En matematisk sfære består af utælleligt uendeligt mange punkter.

Hvis man har en utællelig uendelighed og trækker 1 fra, har man stadig uendeligt. På samme måde kan man også have en sfære, der består af utælleligt uendeligt mange punkter og fjerne et af dem. Man kan nemlig "dække over" det manglende punkt med de uendeligt mange andre punkter.

Hvis man fjerner tælleligt uendeligt mange punkter, kan man også dække over det, hvis man har utælleligt uendeligt mange punkter på sfæren. Derfor kan man dele en matematisk sfære op i to på samme måde, som vi kunne dele det uendeligt store sæt af naturlige tal op i to uendeligt store sæt (lige tal og ulige tal).

Dette er en del af konceptet for beviset, men naturligvis ikke det hele. Hele beviset for Banach-Tarski-paradokset kan læses på ProofWiki her.

Populært set er Banach-Tarski-paradokset blevet formuleret som, at man kan skære en appelsin i uendeligt mange stykker og samle stykkerne til to appelsiner. Hver af disse to kan derefter skilles ad og samles igen. På den måde får man efter to runder 4 appelsiner og sådan kan man blive ved - i hvert fald matematisk set.

Vi kan regne ud, hvor mange runder medhjælperne på Smukfest skulle gøre det ved først at udregne, hvor mange appelsiner der blev brugt under sidste års festival:

Først omregner vi den opgivne vægt til gram:

$$126.700 \,\mathrm{kg \, appelsiner}\cdot 1000 \,\mathrm{g/kg}=126.700.000 \, \mathrm{gram \, appelsiner}$$

Så kan vi udregne, hvor mange appelsiner det er, ud fra at en appelsin i gennemsnit vejer 131 g:

$$\frac{126.700.000 \,\mathrm{gram \, appelsiner}}{131\, \mathrm{gram \, pr. \, appelsin}}=967.176 \,\mathrm{appelsiner}$$

Nu kan vi udregne, hvor mange gange man skulle udføre Banach-Tarski-tricket for at få 967.176 appelsiner:

$$2^x=967.176$$

Vi tager den naturlige logaritme på hver side:

$$x \cdot \ln(2)=\ln(967.176)$$

Vi dividerer med \(\ln(2)\):

$$x =\frac{\ln(967.176)}{ \ln(2)}$$

$$x= 19,88$$

Det runder vi op til 20. Hvis Smukfest kun har købt én appelsin, skal de lave Banach-Tarski-tricket à 20 runder for at få appelsiner nok til alle appesinboderne på festivalen - det kræver dog bare, at medhjælperne på festivallen kan dele appelsinerne i uendeligt mange stykker.

Matematikcenter ønsker alle en rigtig god festival!

Kilder:

https://www.reference.com/food/average-weight-orange-dc0ec85723e2b74c

https://www.youtube.com/watch?v=m5A16ezUwhA

https://da.wikipedia.org/wiki/T%C3%A6llelig_m%C3%A6ngde

https://www.youtube.com/watch?v=s86-Z-CbaHA

https://da.wikipedia.org/wiki/Smukfest

http://www.smukfest.dk/media/2509/smukfest-facts-and-figures-2016.pdf

https://proofwiki.org/wiki/Banach-Tarski_Paradox