Hvordan finder man den eneste ene?

"Hvor mange dates skal jeg på, før jeg finder den eneste ene?".

Den tanke har mange singler sikkert haft. Matematikcenter kan ikke love, at den eneste ene findes. Til gengæld kan man med Matematikcenters råd øge chancen for at finde den bedste partner. Vi kan nemlig fortælle, hvornår man skal stoppe med at tænke, at der måske kommer en mere perfekt date senere.

Hvis man gennem sit liv har mulighed for at date 100 personer, har vi regnet ud, at man først skal date 37 personer. Derefter skal man holde fast i den næste person, der er mere perfekt end alle de forrige personer. Chancen for at denne person er den eneste ene, vil være 37 %.

Sådan har vi regnet det ud:

Antagelser:

Vi antager, at man i alt kan date 100 personer igennem sit liv. Vi kalder det samlede antal mulige dates for \(N\), dvs. \(N=100\). Af dem vil der være én person, der er den bedst mulige partner - den eneste ene. Denne person kalder vi \(n\). Herudover er der også en anden regel: Man kan ikke gå tilbage for at date en person, man tidligere har datet og afvist. 

Sandsynligheden for at finde den eneste ene, hvis vi bare valgte en tilfældig person er \( \frac{1}{N} \), så det vil sige, at chancen for at vælge den eneste ene tilfældigt altså kun 1 %. Det er ikke en særlig stor chance, så vi skal se på, hvordan man kan øge denne chance.

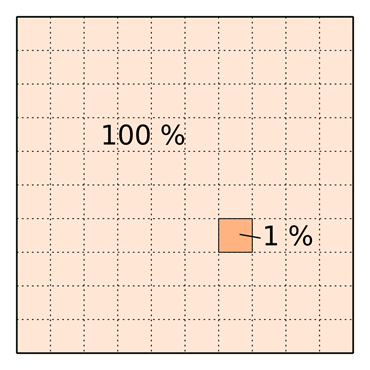
Når man går på et antal dates, kommer der et tidspunkt, hvor det kan betale sig at stoppe med at afvise sine dates og derefter vælge den næste, der har mere potentiale end alle de tidligere dates. Den sidste person, man dater, før man stopper med konsekvent at afvise, kalder vi for \(K\). Dem, man dater efter personen \(K\), kan man acceptere eller afvise, alt efter om de er bedre end alle de tidligere personer eller ej. Man er altså nødt til at gå på date med et antal personer (\(K\)) - det er ikke nok at melde afbud til daten, for man skal vide, hvor kvalificerede partnere de er, så man kan sammenligne efterfølgende kandidater med dem.

Matematikken

Lad os kalde chancen for at vælge den bedste partner for \(P(K)\). Værdien chancen er nemlig afhængig af størrelsen for \(K\), og vi skal finde den \(K\)-værdi, der giver os den bedste chance for at ende op med personen \(n\), den eneste ene.

Denne funktion, \(P(K)\), er summen fra \(1\) til \(N\) af to andre sandsynligheder ganget sammen, nemlig sandsynligheden for at møde den eneste ene på hver date og sandsynligheden for at, man vurderer, at denne person er den eneste ene og derfor vælger at forblive sammen med personen. Vi kalder de to sandsynligheder for \(P(\mathrm{meet\, n})\) og \(P(\mathrm{choose\, n})\). Summen er derfor:

$$\mathrm{P(K)} = \sum_{n=1}^{N} \mathrm{P(meet\, n)}\cdot \mathrm{P(choose \, n)}$$

\(P(\mathrm{meet \, n})\) er \(\frac{1}{N}\), uanset størrelsen af \(K\).

Lad os se på \(P(\mathrm{choose \,n})\): Hvis den eneste ene (\(n\)) er blandt personerne til og med \(K\) (n≤K), er sandsynligheden for at ende op med den eneste ene lig 0, fordi man afviser alle disse personer. Man ved jo ikke, at det er den eneste ene og at alle de kommende dates vil være dårligere end denne.

$$\sum_{n=1}^{N} \mathrm{P(meet\, n)}\cdot \mathrm{P(choose \, n)} = 0 \,\mathrm{for\, n≤K}$$

Hvis den eneste ene derimod kommer lige efter \(K (n=K+1)\) er der 100 % chance for, at vi vælger den eneste ene. Men hvad hvis den eneste ene fx har nummer \(K+1, K+2, K+3, ..., N-1\) eller \(N\)?

For at finde \(P(choose \, n)\) for \(n>K\) skal vi se på sandsynligheden for, at den person, der har mest partnerpotentiale blandt de \(n-1\) første personer er blandt de første \(K\) personer. Hvis det er tilfældet, vil man nemlig ende op med den eneste ene. 

Sandsynligheden for at den bedste date blandt de \(n-1\) personer er fx person nr. 1 er \(\frac{1}{n-1} \). Der er samme sandsynlighed for at det er person nr. \(2, 3, ... n-2\) eller \(n-1\). Vi vil se på sandsynligheden for at personen er blandt de \(K\) første personer, så vi får sandsynligheden

$$P(\mathrm{choose\, n})=K \cdot \frac{1}{n-1} = \frac{K}{n-1} \mathrm{for \ n>K}$$

Det betyder, at vi kan skrive vores sum som

$$\sum_{n=1}^{N}=\frac{1}{N}\cdot\left\{\begin{matrix} 0,\mathrm{for\, n}\leq K\\ \frac{K}{n-1},\mathrm{for\, n}>K \end{matrix}\right.$$

Vi ser nu blot på tilfældet, hvor \(n>K\). Vi omskriver udtrykket:

$$P(K)=\sum_{n=K+1}^{N} = \frac{1}{N} \cdot \frac{K}{n-1} = \frac{K}{N}\cdot \sum_{n=K+1}^{N} \frac{1}{n-1} \\ = \frac{K}{N}( \frac{1}{K}+  \frac{1}{K+1}+ ...+\frac{1}{N-1})$$

Indmaden i parentesen i den sidste del af udtrykket udvikler sig på samme måde som arealet under grafen for funktionen \(\frac{1}{x}\), og tilnærmælsen bliver mere præcis, når N går mod uendeligt.

$$\int_{K}^{N}\frac{1}{x}\, dx$$

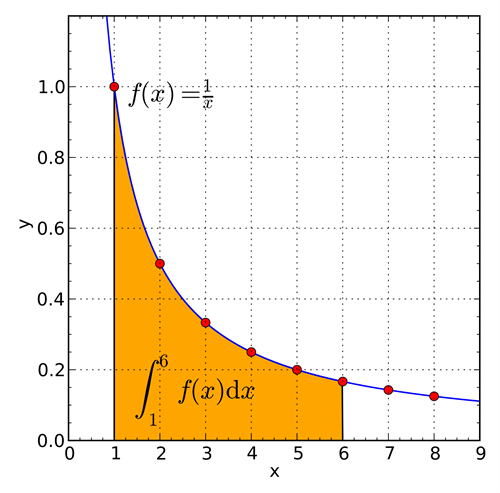
Hele udtrykket kan derfor skrives som

$$ \frac{K}{N} \cdot \int_{K}^{N} \frac{1}{x}\, dx = \frac{K}{N}\cdot \begin{bmatrix} \mathrm{ln}(x) \end{bmatrix}_{K}^{N} = \frac{K}{N}\cdot \mathrm{ln}\left ( \frac{N}{K}\right )$$

Vi laver en substitution:

$$x = \frac{K}{N}$$

Så kan udtrykket omskrives: $$x \cdot \mathrm{ln}\left ( \frac{1}{x}\right ) = -x \cdot \mathrm{ln}(x)$$

Denne funktion betegner, hvor stor chancen er for at finde den eneste ene ved forskellige \(K\)-værdier. For at finde den \(K\)-værdi, der giver størst chance for succes, differentieres funktionen, hvorefter vi løser ligningen \(\frac{\partial }{\partial x}=0\):

$$\frac{\partial }{\partial x}(-x\cdot \mathrm{ln}(x)) = -1 \cdot \mathrm{ln}(x)-x \cdot\frac{1}{x} = -\mathrm{ln}(x)-1$$

$$-\mathrm{ln}(x)-1=0\Leftrightarrow \mathrm{ln}(x)=-1\Leftrightarrow x=\mathbf{e}^{-1} = 0,368$$

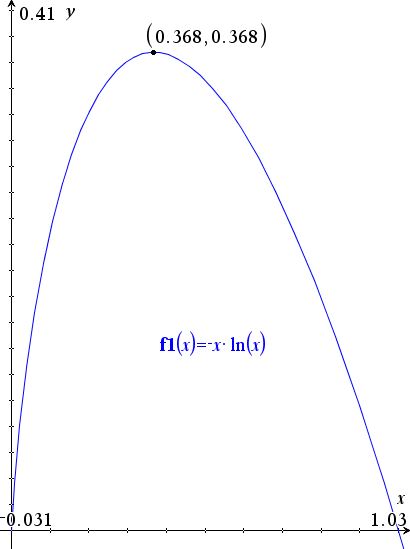
Det vil sige, at når \(x = 0,37\), vil sandsynligheden være højest for at vælge den eneste ene. Det vil sige:

$$\frac{K}{N} = 0,37 \Leftrightarrow K=0,37\cdot N$$

Når \(N=100\) er den optimale \(K\)-værdi 37. Det vil sige, at man skal date 37 personer og afvise dem, og derefter slå sig ned med den efterfølgende person, der har mere potentiale end alle de foregående. Det vil også sige, at der med denne metode er 37 % chance for at ende op med den eneste ene. Det er altså væsentligt højere end hvis man blot valgte en tilfældig person ud af de 100 mulige.

Matematikcenter ønsker alle en god Valentine's Day. 

Kilder:

http://www.math.uah.edu/stat/urn/Secretary.html

https://www.youtube.com/watch?v=XIOoCKO-ybQ