NCC Tømrer

Entreprenørvirksomheden NCC har siden 2015 været Matematikcenters hovedsponsor. I Matematikcenter arbejder vi for at skabe begejstring og bedre forståelse for matematik og naturvidenskab blandt børn og unge. Gennem samarbejdet med NCC vil vi vise potentialet i en erhvervsrettet eller teknisk uddannelse.

Pythagoras i hverdagen

De fleste har hørt om Pythagoras læresætning, men det er nok de færreste, som rent faktisk har brugt den i andre sammenhænge end skolen. I videoen nedenfor ser vi Daniel, som er ansat som tømrersvend hos NCC, og hvordan han benytter Pythagoras til daglig. 

Et eksempel

Vi prøver samme metode som Daniel, bare med nogle lidt andre værdier. 

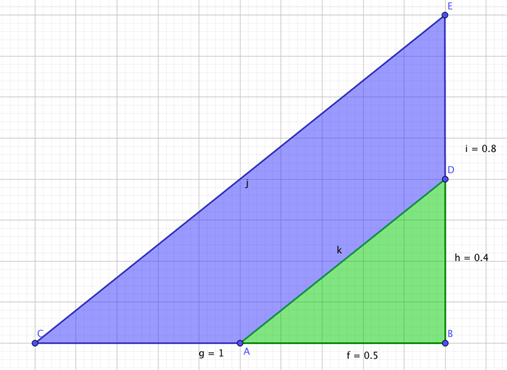
Som det ses på tegningen, så er linjestykket BE den nye væg vi gerne vil sætte. For at gøre det hurtigt, så kan man ud fra linjestykket BC og lidt matematik gøre det ret nemt. Den nye væg skal være vinkelret på den eksisterende væg, altså vinkel B skal være 90°. Hvis der eksisterer en ret vinkel i en trekant, så må man benytte Pythagoras læresætning til at bestemme sidelængderne. Pythagoras læresætning siger,

$$ a^2+b^2=c^2 $$

Hvor a og b er de korte sider fra den rette vinkel. De kaldes kateter. Den lange side som ligger overfor den rette vinkel, kaldes hypotenusen. 

Vi starter med den grønne trekant. Hvis man kender to sidelængder, så kan man altså finde den sidste. Vi ved hvor den nye væg skal starte, punktet B. Vi kender også kateternes længde, så derfor kan vi lave regnestykket

$$ c^2 = 0.5^2+0.4^2 = 0,41$$

Vi kender nu \( c^2 \). For at bestemme længden på c, så skal vi have potensen fjernet. Det gør vi ved at tage kvadratroden til \( c^2 \), da \( \sqrt{x^2} = x \).

$$ \sqrt{0,41} = 0,64 $$

Vi kan gøre præcis de samme for den blå trekant, hvor man skal huske at den grønne blot udgør en del af den store blå trekant. 

$$ 1^2+0.8^2 = \sqrt{1.64} = 1.28 $$

Når man har lavet disse udregninger, så kan man simpelt måle efter med sin tommestok, og dermed sikre sig, at man får sat væggen korrekt.