Tak for kaffe

En kop varm kaffe til at starte dagen er altid godt. Men hvor længe skal man egentligt vente før kaffen har fået den perfekte drikketemperatur?

Segafredo er en af de virksomheder, der støtter Matematikcenters arbejde for at udbrede matematik til alle.
Vi tog derfor fat i dem for at høre, hvordan man laver den bedste kop kaffe. De fortalte os, at der grundlæggende er tre ting man skal have helt styr på:

• Bryggetemperaturen skal være mellem \(94^{\circ}C\) og \(96^{\circ}C\)
• Malingsgraden er vigtig. Eksempelvis skal kaffe, der anvendes til stempelkaffe males grovere end filterkaffe
• Forholdet mellem vand og kaffepulver er essentiel. Til filterkaffe skal der bruges 7 gram kaffe per kop

Efter man har fulgt denne guide - og brygget sig selv en perfekt, dampende kop mocca, hvor længe skal man så vente før den har nået den perfekte drikketempreratur?

For at svare på det skal vi have fat i Newtons Afkølingslov.

Det bliver dog hurtigt nogle ret lange udregninger, hvor man skal have en anelse kendskab til Matematik A på gymnasielt niveau. Så hvis du ikke har lyst til at kæmpe dig igennem en masse matematik, kan du få svaret lige her: Man skal nemlig vente 16 minutter og 42 sekunder før kaffens temperatur rammer plet.

Hvis du til gengæld er interesseret i, hvordan vi er kommet frem til svaret, så er det bare om at læse videre.

 

Sådan har vi regnet det

Matematisk udtryk

"Hastigheden hvormed temperaturen af et legeme ændres, er proportional med forskellen mellem legemets temperatur og det omgivende rums temperatur"

Ovenstående er netop Newtons afkølingslov. Lad os dele loven op, så vi på baggrund af den kan opstille et matematisk udtryk.

Den starter med: "Hastigheden hvormed temperaturen af et legeme ændres (...)". Hastigheden hvorved noget ændrer sig kan netop beskrives som en differentialkvotien. Altså:
$$\frac{d\, T}{d\, t}$$

Herefter fortsætter den: "(...) Denne hastighed er således proportional med forskellen mellem legemets temperatur og det omgivende rums temperatur."
Vi skal altså have en proportionalitetskonstant ganget på forskellen i temperatur mellem væsken og omgivelserne.
$$k\, \left(M - T\right) $$

Her er T en funktion af tiden, t. Altså menes der T(t).

Vi har altså:
$$ \frac{d\, T}{d\, t} = k\; \left(M - T\right) $$

Differentialligning

Der er altså tale om en differentialligning. Ligningen er faktisk af en type som vi umiddelbart kan slå op i tabellen under "Løsninger til differentialligninger". Men vi kan også selv ret hurtigt finde en løsning til den blot ved at anvende gættemetoden.

Først samler vi alle led indeholdende T(t) på samme side:
$$ \frac{d\, T}{d\, t} + k\,T = k\,M $$

Den homogene ligning

For at løse differentialligningen starter vi med at anskue den tilhørende homogene ligning:
$$ \frac{d\, T}{d\, t} + k\,T = 0 $$

Et godt gæt på en løsning i denne sammenhægn ville være
\(T(t) = c\,e^{-k\cdot t},\; c\in\mathbb{R}\).
Hvor c er en arbitrær reel konstant. Grunden til at vi vælger at gætte på denne løsning skyldes, at den differentierede eksponentialfunktion netop bliver: \(\frac{d\, T}{d\, t} = -c\;k\;e^{-k\cdot t}\).

Vi gør prøve for at se om dette er opfylder vores ligning:
$$ -c\,k\,e^{-k\cdot t} + k\,c\,\,e^{-k\cdot t} = 0 $$
Altså er det opfyldt.

Den inhomogene ligning

Nu forsøger vi så at finde løsningen til vores inhomogene ligning. Igen anvender vi gættemetoden:
$$ \frac{d\, T}{d\, t} + k\,T = k\,M $$
Et passende gæt er netop en funktion, der ikke er afhængig af t, da den så forsvinder, når vi differentierer den. Et godt gæt er altså: \(T(t) = M\).

Vi gør igen prøve for at se om det passer:
$$ 0 + k\;M = k\;M $$

Hvilket ganske givet også er opfyldt.

Ved at anvende superpositionsprincippet kan vi nu opskrive den fuldstændige løsningsmængde:

$$ L_{inhom} = \{M + c\,\,e^{-k\cdot t}|c \in \mathbb{R}, \; t \in \mathbb{R}, \; k \in \mathbb{R}\} $$

 

Betinget løsning

Efter at have opskrevet løsningen til vores differentialligning gør vi nu det hele en anelse mere konkret igen.

I vores løsning har vi nemlig det problem, at der fremgår to ukendte parametre som vi skal bestemme: c og k. Vi har indtil videre nemlig bare opskrevet den generelle løsning.
Det er dog ikke den løsning vi er interesserede i. I stedet vil vi gerne finde en betinget løsning for vores situation. Vi skal således bruge to startbetingelser for at kunne bestemme de to konstanter, der indgår.

Forsøg

Vi finder de to startbetingelser ved at lave et lille forsøg.

Vi brygger en lækker kop kaffe og måler dens temperatur lige idét vi har hældt den i koppen - altså til tiden t = 0. Herefter venter vi 20 minutter og 30 sekunder, hvorefter vi igen måler temperaturen.

Ved det lille forsøg bestemte vi følgende konstanter:

\(\mathrm{Stuetemperatur}: \; M = 20^{\circ}C\)
\(\mathrm{Temperatur\; ved\;} t = 0: \; T(0) = 89^{\circ}C\)
\(\mathrm{Temperatur\; ved\;} t = 1230: \; T(1230) = 54^{\circ}C\)

Konstanter

Med informationen fra vores forsøg kan vi nu bestemme konstanterne i vores ligning.
Vi ved at til tiden t = 0 er kaffen \(89^{\circ}C\). Altså:
\(T(0) = 20 + c\,\,e^{-k\cdot 0} = 20 + c = 89 \)

\(c = 69\)

 

Nu mangler vi bare at bestemme k, så har vi vores løsning. Her udnytter vi vores anden måling fra forsøget. Vi ved at til tiden t = 1230 er kaffen \(54^{\circ}C\):

\(T(1230) = 20 + 69\,e^{-k\cdot 1230} = 54\)

\(20 + 69\,e^{-k\cdot 1230} = 54 \Leftrightarrow  e^{-k\cdot 1230} = \frac{34}{69} \)

\( e^{-k\cdot 1230} = \frac{34}{69} \Leftrightarrow k = \frac{\ln\left(\frac{34}{69}\right)}{1230}\)

Numerisk har k således værdien:

\(k = 0{,}0006\)

 

Langt om længe har vi altså bestem et udtryk for kaffens temperatur som funktion af tid.

\(T(t) = 20 + 69\,e^{-0{,}0006\, t}\)

Grafen for denne funktion ser således ud:

 

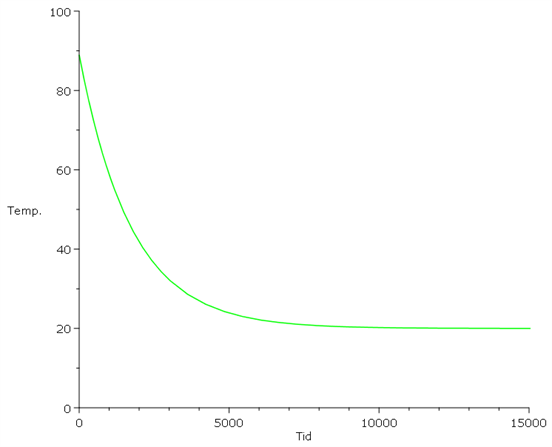
Det er her tydeligt, at når \(t \rightarrow \infty\) så går \(T \rightarrow 20\). Sagt på en anden måde: Hvis vi venter længe nok vil kaffen nå stuetemperatur, hvilket giver fin mening. 

I følge et studie fra University of Texas er den optimale drikketemperatur for kaffe \(57{,}8^{\circ}C\). Vi skal nu blot løse vores ligning for den tid, t, det tager før kaffen har nået den pågældende temperatur.

\(20 + 69\,e^{-0{,}0006\cdot t} = 57{,}8\)
\(\Updownarrow\)
\(t = \frac{-\ln\left(\frac{37{,}8}{69}\right)}{0{,}0006} = 1003 \)

Det tager altså 1003 sekunder før kaffen har ramt den perfekte drikketempreratur. Hvilket svarer til \(\frac{1003}{60} = 16{,}7\) minutter.