5 års fødselsdag
For fem år siden spredte Mattecentrum sig hen over Øresund, og Matematikcenter blev en realitet. Efter blot et halvt år var der lektiecaféer fire dage om ugen i København, og i løbet af de følgende år er antallet af caféer mere end femdoblet og dækker nu ud over Københavnsområdet også Aalborg, Aarhus, Odense, Roskilde, Silkeborg og Vejle. Samtidig tilbyder vi også online lektiehjælp over chat og her på Webmatematik.dk, der havde sine første besøgende mandag d. 7. oktober 2012
Matematikcenter i tal
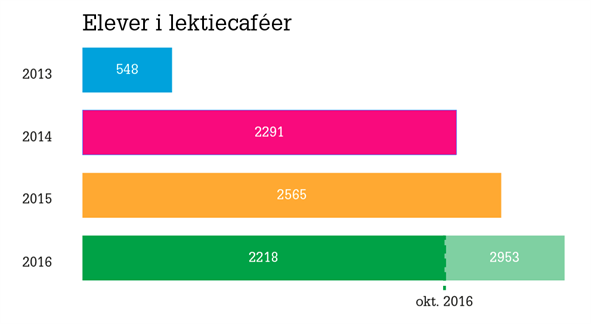
Vi har samlet tal fra vores lektiecaféer siden 2013 og sammenlignet dem, for at se udviklingen i antallet af frivillige og elever. I den første tabel står antallet af frivilligtimer (én frivillig i en time) pr. år overfor antallet af elever i lektiecaféerne. Her er det tydeligt, at vi siden begyndelsen har kunne allokere ca. en times hjælp til hver elev, hvilket giver mulighed for at komme i dybden med de forskellige spørgsmål. At vi allerede nu, med stadig tre måneder tilbage af 2016 er så tæt på tallene fra '15 vidner om, at lektiecaféerne stadig vokser i størrelse over hele landet.
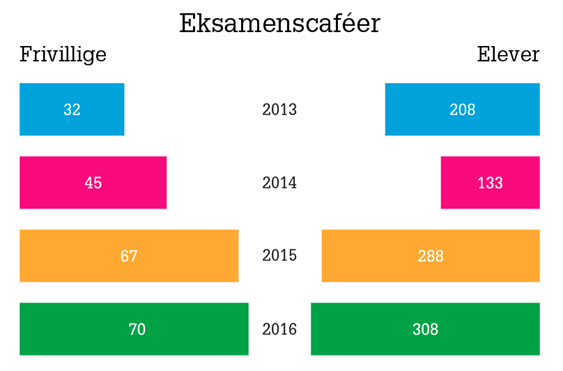
Hvert år har vi desuden afholdt Eksamenscaféer, for på bedst mulig vis at få afklaret de spørgsmål der måtte være i forbindelse med den skriftlige eksamen. Her har vi samlet så mange frivillige og elever som muligt. I 2013 og '14 blev Eksamenscaféen kun afholdt i København. De sidste to år har vi dog udvidet konceptet, så der har været afholdt eksamenscaféer i alle de fire største byer (København, Aarhus, Odense og Aalborg).
Så mange besøger Webmatematik.dk
Siden 2013 har der været 7.653.990 besøg på Webmatematik.dk.
Vi har regnet på, hvordan antallet af besøgende pr. uge her på Webmatematik.dk udvikler sig over tid. Vi kan konstatere, at udviklingen i høj grad følger den logistiske funktion
$$b(t) = \frac{98\ 525}{1+78,59 \cdot e^{-0,037 \ \cdot \ t}}$$
Hvis udviklingen fortsætter vil 2 ud af 3 studerende på ungdomsuddannelser bruge Webmatematik.dk én gang om ugen i 2020.
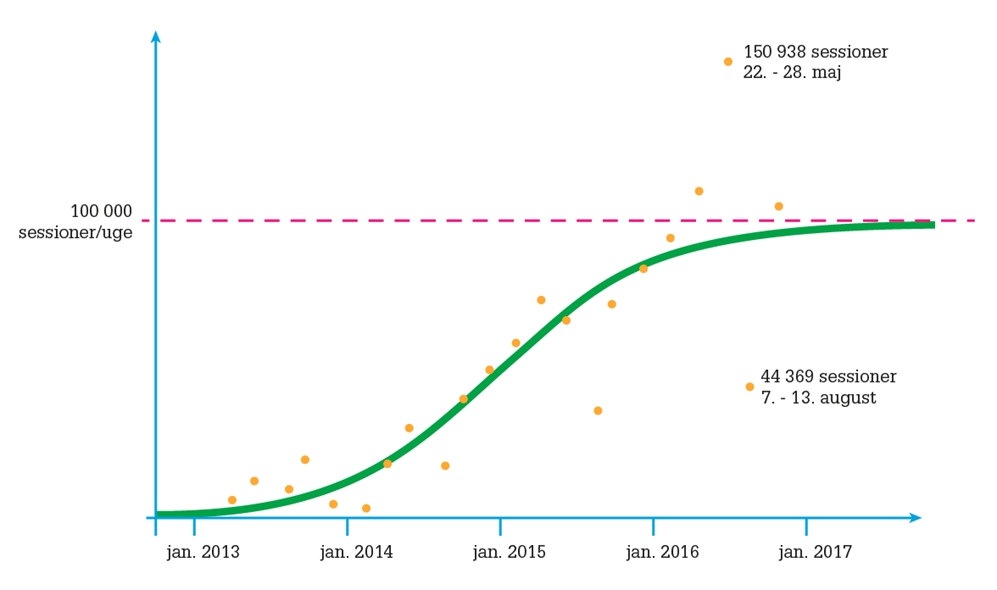
Antallet af sessioner er et udtryk for, hvor mange bruger Webmatematik.dk, og skal ses i forhold til antallet af sidevisninger, der er hvor mange unikke sider, der er blevet læst. Dette tal er over 23 millioner siden 2012!
Sådan har vi regnet det ud
Det første skridt mod at bestemme en funktion for udviklingen, er at plotte de mange datapunkter i et koordinatsystem. På nedenstående billede er dette gjort, hvor førsteaksen betegner antal uger efter hjemmesidens lancering, og andenaksen er antallet af sessioner den pågældende uge.
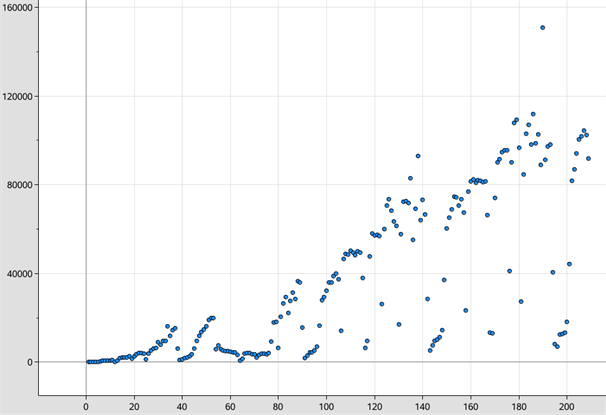
Fra datasættet ses både en tydelig stigning i antallet af besøgende, og en række datapunkter, der ikke følger den generelle trend. Særligt fra uge 90 og frem er disse anomalier tydelige. Ved at sammenholde datapunkterne med en kalender, viser det sig dog at punkternes ugetal er identisk med skolernes ferier. Selvom man skal være varsom med at fjerne datapunkter når man arbejder videnskabeligt, så kan man godt fjerne tilfælde, hvor betingelserne ikke er de samme, f.eks. hvis eleverne ikke er i skolen og derfor ikke har brug for hjælp til matematik. Datapunkterne koresponderende med efterårs-, jule-, vinter-, påske- og sommerferien er derfor ekskluderet fra beregningerne. Nedenstående billede viser datasættet uden ferieugerne.
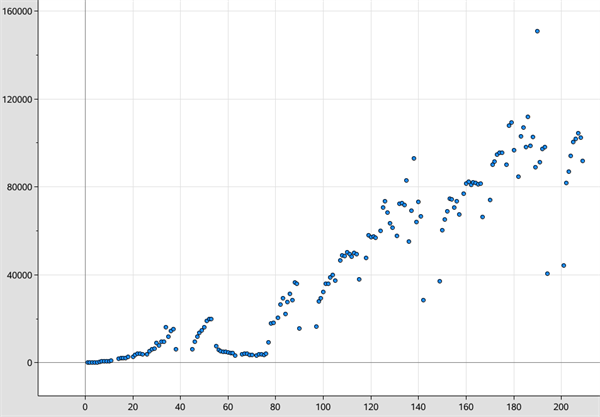
Der er stadig lidt spredning, men de ekstreme 'outliers' forårsaget af ferier er væk.
Når man arbejder med vækst vil eksponentiel vækst være det umiddelbare valg, men ofte mimerer logistisk vækst virkeligheden i langt højere grad. Dette skyldes, at grafen for en logistisk vækst går mod et 'steady state', altså en øvre grænse.
Læs mere om logistisk vækst her: logistisk vækst og differentialligninger
For at finde den bedst passende logistiske funktion anvender vi logistisk regression. Den fundne funktion er indtegnet i nedestående billede med rød. For at have en sammeligningsgrundlag har vi også indtegnet den bedst passende eksponentialfunktion med grøn. Det bliver således tydeligt, at den logistiske vækst i langt højere grad afspejler den overordnede udvikling.
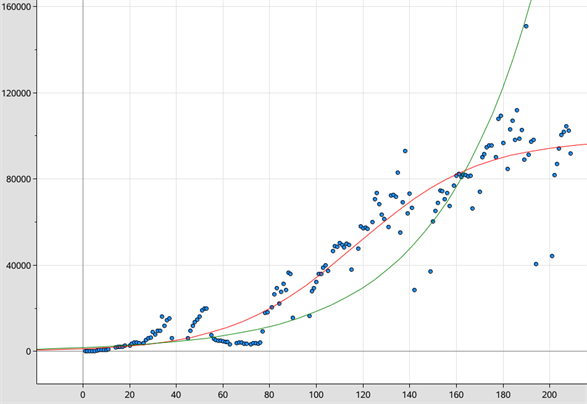
Ud fra forskriften for den fundne logistiske funktion kan vi aflæse den grænseværdi, eller 'steady state', som antallet af sessioner vil nærme sig. Dette tal er brøkens tæller, idet nævneren går mod \(1\), når den uafhængige variabel går mod \(\infty\). Med andre ord, så er $$M = \lim_{x\to\infty}(\frac{M}{1+ce^{-aMx}})$$ Den funktion som beskriver antallet af sessioner er $$b(t) = \frac{98\ 525}{1 + 78,59 \cdot e^{-0,037 \ \cdot \ t}}$$ og grænseværdien kan her aflæses til at være \(98\ 525\). Dette tal svarer til \(\frac{98\ 525}{155\ 947} \cdot 100 \% = 63,18%\) af alle studerende på alle ungdomsuddannelser i år 2015. Med andre ord, så vil to-tredjedele af alle studerende på alle ungdomsuddannelser besøge webmatematik hver uge.
Da \(b(t)\) aldrig kan være lig \(98\ 525\), så vil vi undersøge, hvornår \(b(t) = 98\ 524\), for at finde ud af, hvornår det maksimale antal besøgende (stort set) er opnået. Dette gøres ved at løse ligningen med hensyn til \(t\).
\(\frac{98\ 525}{1 + 78,59 \cdot e^{-0,037 \ \cdot \ t}} = 98\ 524 \Leftrightarrow\)
\(98\ 525 = 98\ 524 + 98\ 524 \cdot 78,59 \cdot e^{-0,037 \ \cdot \ t} \Leftrightarrow\)
\(\frac{1}{98\ 524 \cdot 78,59} = e^{-0,037 \ \cdot \ t} \Leftrightarrow\)
\(\frac{\ln(\frac{1}{98\ 524 \cdot 78,59})}{-0,037} = t\)
\(429,22 = t\)
Det maksimale antal besøgende vil blive nået 429 uger efter hjemmesidens lancering i oktober, svarende til d. 28 december 2020.
Samlet hjælp givet indtil nu i 2016
Selvom 2016 ikke helt afsluttet endnu, så har vi taget et kig på året for at se, hvor meget hjælp vi har givet indtil nu. Det viste sig at være 12,774 ugers konstant lektiehjælp. Derudover er der samlet blevet brugt næsten 28 års samlet tid på Webmatematik.dk.
Udregning
Indtil videre har der været afholdt lektiecaféer landet over i 18 uger, da der har været lukket i forbindelse med diverse ferier og helligdage. I løbet af de 18 har vores fantastiske frivillige tilsammen lagt 2146 timer i caféerne. For at få det i uger dividerer vi det med produktet af antal timer på et døgn og døgn på en uge.
$$\frac{2146 \ timer}{24 \frac{timer}{døgn}\cdot 7 \frac{døgn}{uge}} = 12,774 \ uger$$
Den samme fremgangsmåde har vi brugt for at finde ud af, hvor lang tid, der er blevet brugt på Webmatematik.dk i alt. Dog skal den gennemsnitlige sessionslængde dog først ganges med antallet af sessioner i løbet af 2016. De to tal er hhv. \(3\ 209\ 426\) sessioner og \(4\) minutter og \(34\) sekunder \(= 4,57\) minutter.
$$\frac{3\ 209\ 426 \ sessioner \cdot 4,57 \frac{minutter}{session}}{60 \frac{minutter}{time} \cdot 24 \frac {timer}{døgn} \cdot 7 \frac{døgn}{uge} \cdot 52 \frac{uger}{år}} = 27,98 \ år$$
