Badering
I denne varme er der ikke meget, der er bedre end en tur på stranden. Når man har læst vores guide til, hvor tykt ens solcreme-lag skal være og har styr på antallet af sandkorn på en strand, er man klar til at gå i vandet.
Måske gør man det med en stor oppustelig luftmadras, med et krokodilleformet badedyr eller med en stor badering, som man kan ligge og dase i.
Vi har regnet ud, at man skal bruge 37,4 mundfulde luft på at puste en stor badering op.
Sådan har vi regnet det ud:
Vi har taget udgangspunkt i denne store badering, som har en diameter på 106 cm. En badering har normalt form som en torus, som også kaldes en ringflade - eller en donutform. En torus konstrueres ved at dreje en cirkel hele vejen rundt om en akse, som ligger uden for cirklen selv.

Vi er interesseret i at finde rumfanget af baderingen, så vi kan udregne, hvor mange gange, man skal trække vejret for at få den fyldt med luft. Rumfanget af en torus findes med formlen \(V_{torus}=2 \cdot\pi^2\cdot R\cdot r^2\)
Her er \(r\) lig med radius for den cirkel, der blev roteret omkring aksen, mens \(R\) er afstanden mellem torussens centrum og centrum i den cirkel, der blev roteret om aksen.
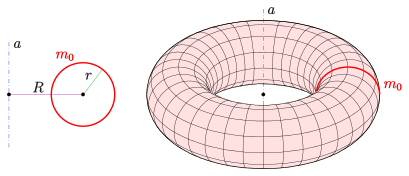
Vi skal finde \(r\) og \(R\) for baderingen. På det forstørrede billede på hjemmesiden målet baderingen 14,6 cm i diameter. I virkeligheden er den 106 cm i diameter. 1 cm på tegningen svarer altså til \(\frac{106 \,\mathrm{cm}}{14,6 \,\mathrm{cm \, på \, billedet}}=7,26 \, \mathrm{cm\, pr.\, cm \, på\, billedet}\)
Ved at bruge dette målestoksforhold kan vi finde de to radii. Vi udregner \(r\) ved at måle diameteren af hullet i midten af baderingen, da det er lettere at måle. Den får vi til 6 cm. Diameteren af torussen er diameteren af hullet i midten lagt sammen med \(4\cdot r\).
Derfor må \(4 \cdot r\) være lig med \(14,6\,\mathrm{cm}-6\,\mathrm{cm}=8,6\,\mathrm{cm}\).
Vi udregner størrelsen af \(r\) på billedet: \(r=\frac{8,6\,\mathrm{cm}}{4}=2,15\,\mathrm{cm}\).
Vi ganger med vores målestoksforhold:
\(r=2,15\,\mathrm{cm \, på \,billedet} \cdot 7,26\, \mathrm{cm\, pr.\, cm \, på\, billedet}=15,6 \, \mathrm{cm}\).
Så skal vi finde \(R\), som er lig med \(r\) lagt sammen med radius af hullet i midten. Radius af hullet i midten er \(\frac{6 \, \mathrm{cm\, på \, billedet}}{2}=3 \, \mathrm{cm\, på \, billedet}\).
\(R\) er altså \(2,15\, \mathrm{cm\, på \, billedet}+3\, \mathrm{cm\, på \, billedet}=5,15\, \mathrm{cm\, på \, billedet}\)
Vi ganger med vores målestoksforhold:
\(R=5,15\,\mathrm{cm \, på \,billedet} \cdot 7,26\, \mathrm{cm\, pr.\, cm \, på\, billedet}=37,4 \, \mathrm{cm}\).
Nu kan vi regne rumfanget af baderingen med \(V_{torus}=2 \cdot\pi^2\cdot R\cdot r^2\):
\(V_{torus}=2 \cdot\pi^2\cdot 37,4 \, \mathrm{cm}\cdot 15,6 \, \mathrm{cm}^2=179.660 \, \mathrm{cm^3}\).
Vi har nu fundet rumfanget af baderingen.
Når man trækker vejret normalt, ventileres normalt cirka 0,5 L luft.
Hvis man tager en indånding, der er så dyb som muligt og puster ud så kraftigt som muligt, kan man dog puste cirka 4,8 L luft ud.
Vi udregner, hvor mange gange man skal udånde 4,8 L luft, før man har fyldt baderingen med luft. Vi husker, at 1 L er 1000 cm\(^3\):
\(\frac{179.660 \, \mathrm{cm^3}}{4.800 \, \mathrm{cm^3\, pr.\, pust}}=37,42\, \mathrm{pust}\)
Man skal altså puste cirka 37,4 gange, før den store badering er fyldt med luft.
Kilder:
http://www.gucca.dk/stor-badering-med-haandtag-106-cm-p319596
http://www.medviden.dk/kurser/basalfag/fysiologi/basal-respirationsfysiologi/
