2. søndag i advent
Sidste uges adventskonkurrence gik ud på at gætte, hvor meget bånd, der gik til at pakke tre gaver ind.
Som ugen før kan man bruge matematikken til at komme med et bud på, hvor meget bånd der som minimum er brugt, men man er også nødt til at gætte. Det er nemlig ikke til at se, hvor meget bånd, der fx er gået til sløjfer og krøller.
Lad os se på udregningerne:
Den mindste pakke:
Pakken er en kugle med toppen og bunden skåret af. Gavebåndet vikles to gange rundt. Havde det været en hel kugle, svarer mængden af bånd til to gange cirklens omkreds, dvs. 2(2·π·r).
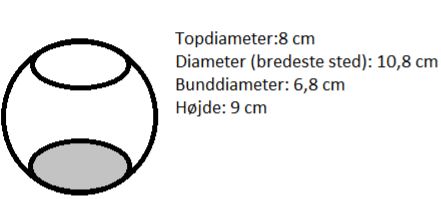
For at finde den rigtige omkreds af kuglen, skal vi fratrække, hvor meget der er fjernet (længden af cirkelbuen, det stiplede stykke herunder) og i stedet lægge diameteren af de to cirkler til (de grønne stykker herunder).
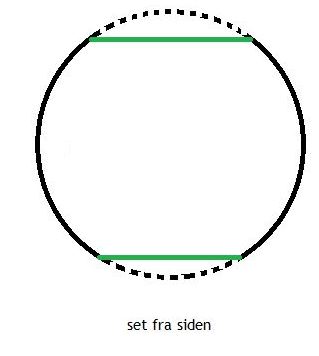
Formlen for længden af en cirkelbue er $$L = 2 \cdot \pi \cdot r \frac{w}{360^{\circ}}$$
For at finde vinklen for hhv. cirkelbuen i toppen og i bunden bruger vi trigonometri:
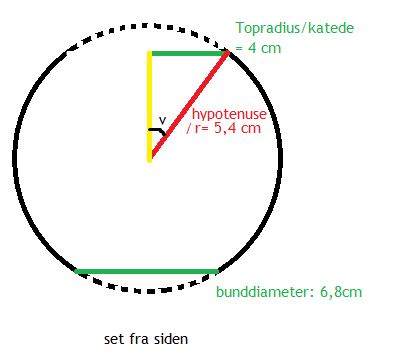
Vi finder vinklen v, der er halv størrelse af vinklen w i formlen for cirkelbuens længde: $$sin(v) = \frac{katede}{hypotenuse}$$
$$sin(v) = \frac{4 cm}{5,4 cm} \Leftrightarrow sin(v)=0,74 \Leftrightarrow v = 47,8 ^{\circ}$$ w har den dobbelte størrelse, dvs. 2·47,8° = 95,6°.
På samme vis kan vi finde vinklen, der afgrænser cirkelbuen i bunden:
$$sin(v) = \frac{\frac{6,8 cm}{2} cm}{5,4 cm} \Leftrightarrow sin(v)=0,63 \Leftrightarrow v = 39 ^{\circ}$$
Det giver os en vinkel w på 39°+39°= 78°.
Vi kan nu finde længden af cirkelbuerne:
Top: $$L = 2 \cdot \pi \cdot 5,4 cm \frac{95,6^{\circ}}{360^{\circ}} = 9 cm$$
Bund: $$L = 2 \cdot \pi \cdot 5,4 cm \frac{78^{\circ}}{360^{\circ}} = 7,4 cm$$
Det vil sige, at der i hvert fald er brugt
O =2(2·π·5,4 cm -(9 cm + 7,4 cm)+ 6,8 cm + 8 cm) = 64,7 cm gavebånd. Hertil kommer sløjfe og krøller.
Den mellemstore pakke:
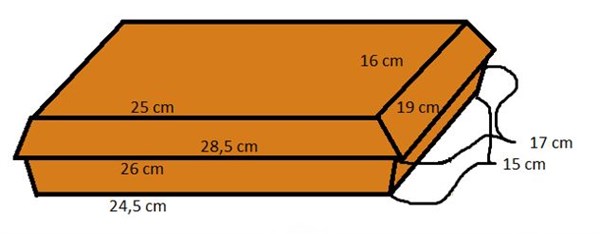
Her vikles gaven ind med bånd rundt på begge leder. Vi ser først på målene, når båndet vikles om gaven på langs:
Bunden er 24,5 cm lang, og toppen er 25 cm lang. Vi ved ikke, hvor høj pakken er. Derfor kan vi kun regne ud, at der skal bruges 49,5 cm bånd på den led.
Når båndet vikles om gaven på langs: Her er det 16 cm + 15 cm = 31 cm. Vi ved igen ikke, hvor høj pakken er.
Der bliver altså brugt 31 cm + 49,5 cm bånd på gaven (dvs. 80,5 cm) + hvad der skal til for at der også kommer bånd på siderne - et kvalificeret bud kunne ud fra tegningen være fx 10 cm i hver side, dvs. 40 cm ekstra i alt. Derudover er der også sløjfe og krøller, der skal tælles med.
Den store pakke:
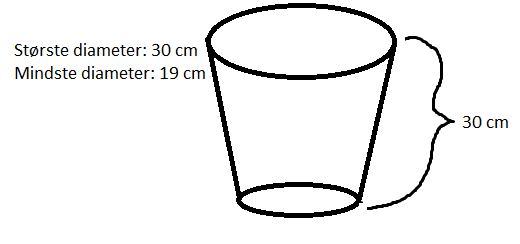
Den store pakke er en keglestub, og båndet vikles omkring den i en cirkel.

Omkredsen på det bredeste sted (med diameter = 15 cm) er 2·π·15 cm = 94 cm, mens den på det smalleste sted er 2·π·9,5 cm = 60 cm. Som det ses i videoen, er båndet sat på den nederste del, men vi ved ikke nøjagtig, hvor højt oppe det sidder. Et kvalificeret bud kunne være fx 80 cm. Hertil kommer igen sløjfe og krøller.
Samlet:
I alt giver vores udregninger: 64,7 cm + 31 cm + 49,5 cm + 40 cm +80 cm = 265,2 cm. Det er dog langt fra svaret, da der bruges meget bånd til at lave sløjfen og krøllerne.
Sløjfer: Ud fra videoen kunne man gætte på, at hver løkke i en sløjfe består af 25 cm bånd. Det giver 6·25 cm = 150 cm bånd til sløjfer.
Så er vi oppe på 415 cm bånd.
Krøller:
Vi har lavet ret mange krøller på vores gaver. Her skal man naturligvis gætte igen, og et kvalificeret bud kunne være cirka 120 cm bånd på hver gave. Så er vi oppe på 415 cm+ 3·120 cm = 775 cm bånd i alt.
Det rigtige svar:
De 775 cm gavebånd er ikke helt galt: Det rigtige svar er 793 cm i alt - fordelt på 220 cm på den lille pakke, 305 cm på den mellemstore og 268 cm på den store.
