Kontinuitet og differentiabilitet
På B-niveau definerede vi kontinuitet ved at sige, at en funktion var kontinuert, hvis man kunne tegne den uden at løfte blyanten fra papiret. Den definition giver et godt visuelt billede af, hvad en kontinuert funktion er - den er sammenhængende.
Imidlertid er det en definition, det er svært at arbejde med i praksis. Derfor indfører vi på A-niveau en mere matematisk definition.
$$f\text{ er kontinuert}\quad\Leftrightarrow\quad\lim_{x\to a}(f(x))=f(a)$$
Med ord ville man sige "\(f\) er kontinuert hvis og kun hvis grænseværdien af \(f(x)\) for \(x\) gående mod \(a\) er lig med \(f(a)\)".
Det, som definitionen egentlig siger, er, at hvis vi lader vores \(x\)-værdi komme uendeligt tæt på et fast punkt, så skal funktionsværdierne også komme uendeligt tæt på funktionsværdien i det faste punkt.
Definitionen kan måske virke kringlet, men måske kan følgende eksempler vise dig, hvordan den virker, og overbevise dig om, at den er smart.
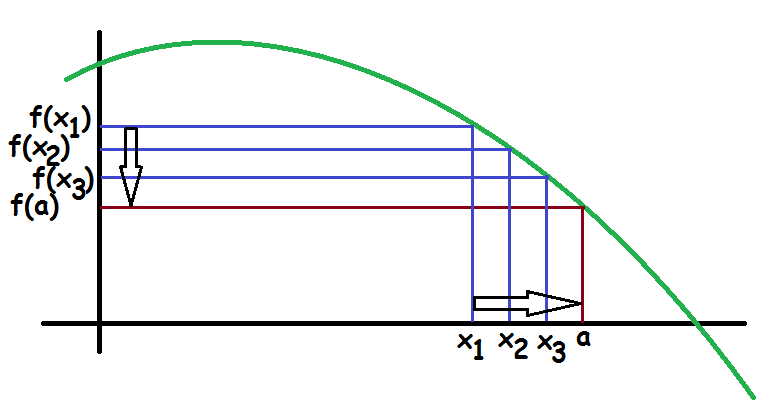
På tegningen herover er tegnet grafen for en kontinuert funktion. Når vi lader vores \(x\)-værdier komme tættere og tættere på det faste punkt \(a\), så kommer funktionsværdierne også tættere på \(f(a\)). Vi kunne gå uendeligt tæt på \(a\), og så ville funktionsværdien også være uendeligt tæt på \(f(a)\).
Bemærk, at vi også kunne have startet med en \(x\)-værdi, der var større end \(a\) og bevæget os mod \(a\) fra højre.
Lad os se på et eksempel, hvor funktionen ikke er kontinuert.
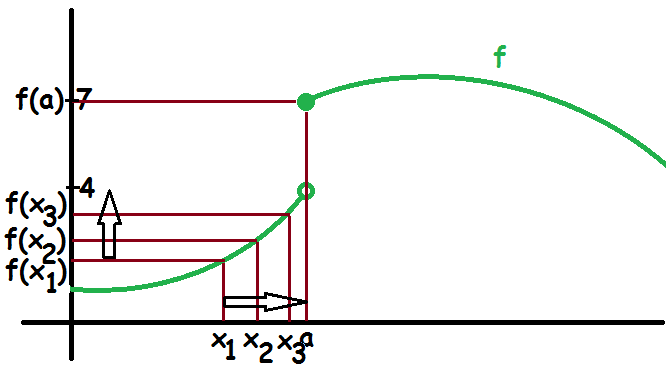
Her kan vi se, at
$$f(a)=7$$
Men lige meget hvor tæt vi kommer på \(a\) med vores \(x\)-værdi (gående fra venstre side), så vil funktionsværdien aldrig blive 7. Den vil i stedet nærme sig 4.
$$\lim_{x\to a^-}(f(x))=4\neq7=f(a)$$
Bemærk, at hvis vi var startet med en \(x\)-værdi, der var større end \(a\) og havde nærmet os \(a\) fra højre, så ville funktionsværdierne nærme sig \(f(a)\). Imidlertid kræves der, at både grænseværdien fra højre og fra venstre giver \(f(a)\), før man kan tale om at en funktion er kontinuert.
Muligvis synes du, at det virker som en løs definition, at nogle tal nærmer sig hinanden uendeligt meget. Vi kan berolige med, at der findes en mere stringent definition, nemlig at en funktion er kontinuert hvis:
$$\forall\varepsilon>0\:\exists\delta>0:|x-a|<\delta\Rightarrow|f(x)-f(a)|<\varepsilon$$
men den slags indviklede sager skal du heldigvis ikke bekymre dig om, medmindre du vil studere matematik på universitetet :-)
Differentiabilitet
På B-niveau lærte vi, at en funktion \(f\) var differentiabel i et punkt \(x_0\), hvis den var kontinuert, og der gjaldt, at dens differens-kvotient
$$a_s=\frac{f(x_0+h)-f(x_0)}{h}$$
havde en grænseværdi for \(h\to0\)
Dette betyder, at der skal være en grænseværdi, både når \(h\) nærmer sig 0 fra venstre og fra højre, og at de to grænseværdier skal være den samme.
Lad os se på et eksempel på en funktion, der ikke er differentiabel.
Vores funktion er
$$f(x)=|x|+2$$
Dens graf er
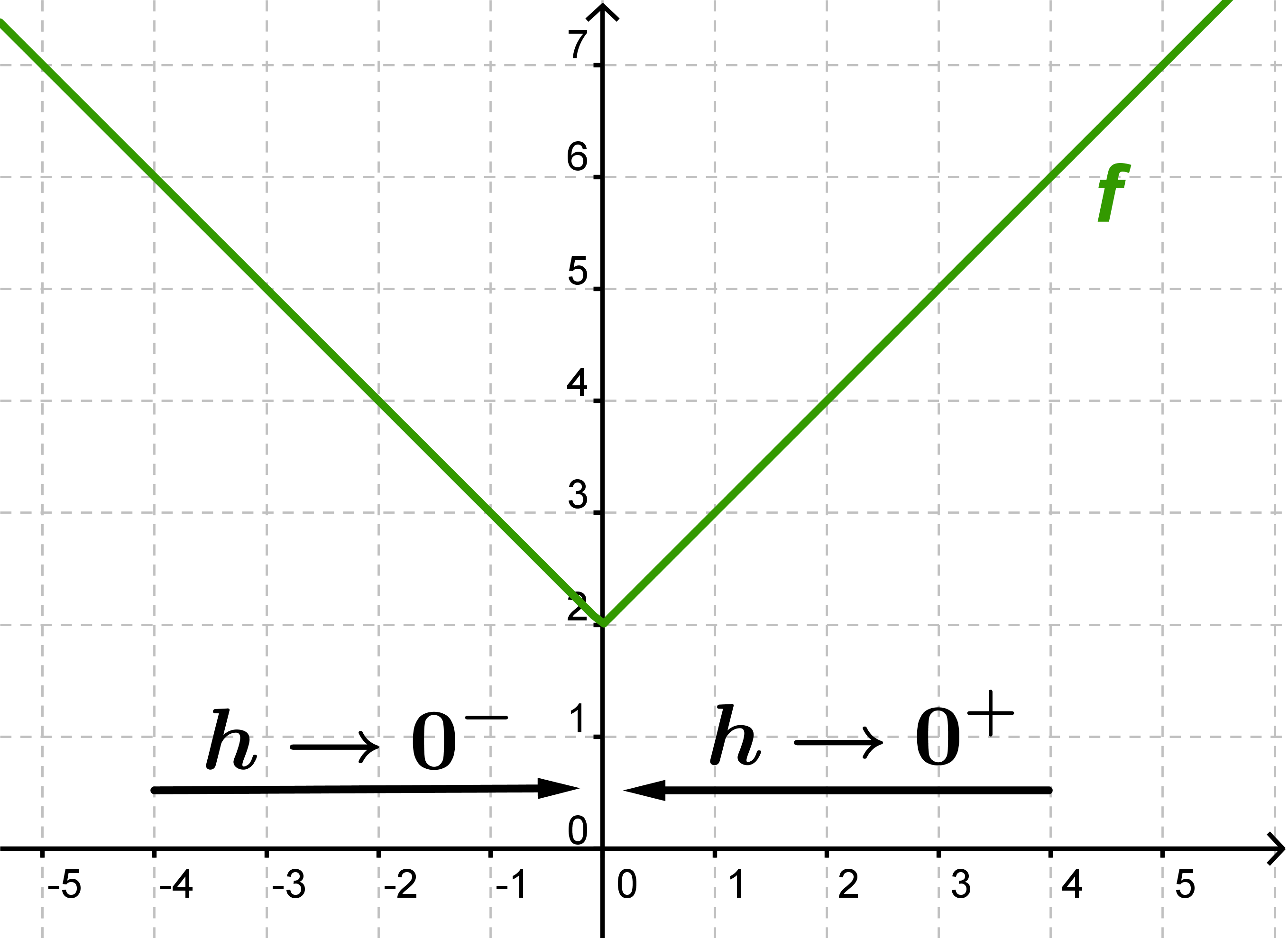
Vi vil se på differentialkvotienten i punktet 0.
Vi bruger tre-trins-reglen.
$$I:\qquad \triangle y=f(x+h)-f(x)=|0+h|+2-(|0|+2)=|h|+2-0-2=|h|$$
$$II:\qquad a_s=\frac{\triangle y}{h}=\frac{|h|}{h}$$
I det tredje trin tager vi grænseværdien for \(h\) gående mod 0 både fra højre og fra venstre.
Vi starter med at tage grænseværdien fra højre. Dvs. at \(h\) er et positivt tal, så \(|h|=h\)
$$III(\text{højre}):\qquad\lim_{h\to0^+}\left(\frac{|h|}{h}\right)=\lim_{h\to0^+}\left(\frac{h}{h}\right)=\lim_{h\to0^+} (1)=1$$
Dernæst tager vi grænseværdien fra venstre. Dvs. at \(h\) er et negativt tal, og derfor er \(|h|=-h\)
$$III(\text{venstre}):\qquad\lim_{h\to0^-}\left(\frac{|h|}{h}\right)=\lim_{h\to0^-}\left(\frac{-h}{h}\right)=\lim_{h\to0^-}(- 1)=-1$$
Fra højre er grænseværdien altså 1 og fra venstre er den -1. Da grænseværdien ikke er den samme, er funktionen ikke differentiabel.
Læg mærke til, at dette stemmer overens med vores B-niveau-definition, hvor vi sagde, at differentiable funktioner ikke måtte have nogen "knæk".
