Skæring mellem plan og kugle

Hvis man har givet et plan og en kugle, kan man være interesseret i at finde ud af, om de to objekter skærer hinanden.

For at afgøre om de skærer hinanden, finder man afstanden mellem kuglens centrum og planen. Dette gøres ved hjælp af formlen for afstand mellem et punkt og et plan.

Man skal holde tungen lige i munden, for man plejer både at kalde kuglens centrum og koefficienterne i planens ligning for a, b og c. For at skelne kalder vi derfor kuglens centrum for

$$C(k_1,k_2,k_3)$$

Vi finder altså afstanden mellem centrum og plan ved formlen

$$\text{dist}(C,\alpha)=\frac{|ak_1+bk_2+ck_3+d|}{\sqrt{a^2+b^2+c^2}}$$

Når man har fundet afstanden, sammenligner man med radius. Der er nu tre muligheder 

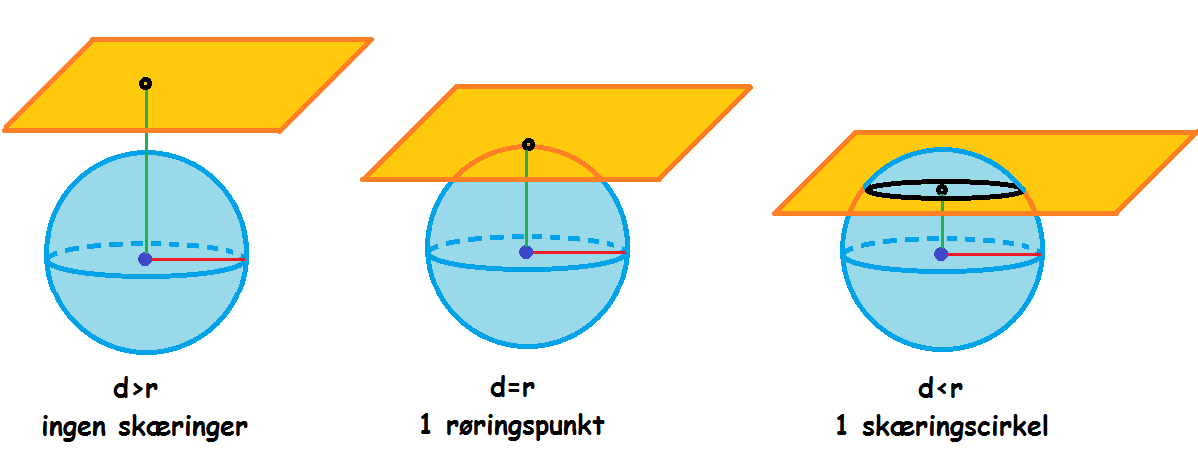
Hvis der kun er et røringspunkt, er planen en tangentplan til kuglen. Hvis planen og kuglen skærer hinanden, vil det altid være i en cirkel. Der findes en formel for, hvordan man udregner ligningen for skæringscirklen, men den er relativt kompliceret, så den springer vi over her.