Afstand mellem kurven for en vektorfunktion og et punkt

Vi betragter en kurve for en vilkårlig vektorfunktion.  Vi ønsker at bestemme den korteste afstand mellem kurven og et givent punkt \(P(x_p,y_p)\) i koordinatsystemet.

Vi kan opskrive vektorligningen, se figur 14:

\(\overrightarrow{R_p}=\overrightarrow{r(t)}+\overrightarrow{r_p(t)}\implies\)
\(\overrightarrow{r_p(t)}=\overrightarrow{R_p}-\overrightarrow{r(t)}=(x_p-x(t), y_p-y(t))\)

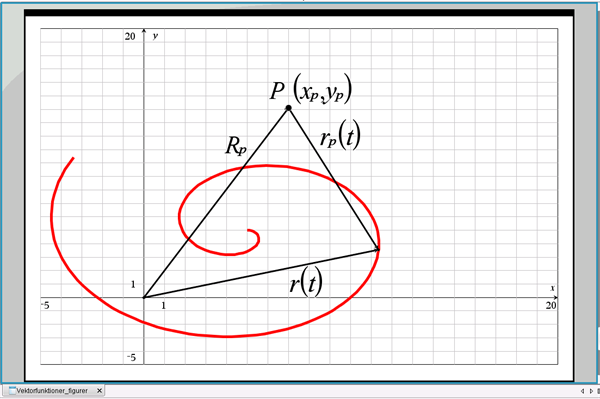
Figur 14    Afstand mellem en kurve og et punkt

Længden af \(\overrightarrow{r_p(t)}\) er da afstanden fra kurven til punkt \(P\), og kvadratet på længden af \(\overrightarrow{r_p(t)}\) er:

\(|\overrightarrow{r_p(t)}|^2 = (x_p-x(t))^2+(y_p-y(t))^2\)
              \(= (x_p^2+y_p^2)+(x(t)^2+y(t)^2)-2\cdot(x_p\cdot x(t)+y_p\cdot y(t))\)

Den korteste afstand mellem kurven og punkt \(P\) fore­kommer for en værdi af \(t\), hvor grafen for højresiden har et minimums­punkt og dermed har vandret tangent. Fra diffe­rential­reg­ningen ved vi, at vi skal differentiere højre siden mht. \(t\) og sætte den afledte funktion lig nul. Herefter skal vi undersøge, om der faktisk er tale om et minimumspunkt og ikke et maksimumspunkt:

\(\dfrac{d}{dt}(|\overrightarrow{r_p(t)}|^2) = 2\cdot x’(t)(x(t)-x_p)+2\cdot y’(t)(y(t)-y_p) = 0\)
\(\implies \dfrac{y’(t)}{x’(t)}=-\dfrac{x(t)-x_p}{y(t)-y_p}=-\dfrac{x_p-x(t)}{y_p-y(t)}\) 

Samme ligning kommer vi frem til, hvis vi betragter problemstillingen rent geometrisk. Den korteste afstand mellem kurven og punkt \(P\) fore­kommer for en værdi af \(t\), hvor \(\overrightarrow{r_p(t)}\) står vinkelret på tangenten til vektorfunktionens kurve. Fra afsnittet om differentiation af vektorfunktion ved vi, at vektoren \(\overrightarrow{v(t)}=(x’(t), y’(t))\) er retningsvektor for tan­genten, og om prikproduktet mellem \(\overrightarrow{r_p(t)}\) og \(\overrightarrow{v(t)}\) gælder da:

\(\overrightarrow{r_p(t)}\bullet\overrightarrow{v(t)}=(x_p-x(t))\cdot x’(t)+(y_p-y(t))\cdot y’(t)=0\)
\(\implies\dfrac{y’(t)}{x’(t)}=-\dfrac{x_p-x(t)}{y_p-y(t)}\)

Eksempel

For Archimedes spiral, se figur 11 i afsnit 5, vil vi finde den korteste afstand til punkt \(P(4,0)\). Vi skal altså søge løsninger til følgende ligning for positive værdier af \(t\):

\(\dfrac{y’(t)}{x’(t)}=\dfrac{2\sin(t)+2t\cos(t)}{2\cos(t)-2t\sin(t)}=-\dfrac{4-2t\cos(t)}{0-2t\sin(t)}\)

Vi løser ligningen vha. et CAS-værktøj, og der er flere løsninger, hvor \(\overrightarrow{r_p(t)}\) står vinkelret på \(\overrightarrow{v(t)}\). Vi ser dog hurtigt, at vi er interesserede i den mindste værdi af \(t\): \(t_0=0,684\), hvor \(\overrightarrow{r(t_0)}=(1,061, 0,865)\), \(\overrightarrow{r’(t_0)}=(0,684, 2,325)\), \(\overrightarrow{r_p(t_0)}=(2,939, -0,865)\) og \(|\overrightarrow{r_p(t_0)}|=3,06\). 

I figur 15 er vist grafen for længden af \(\overrightarrow{r_p(t)}\) som funktion af \(t\), og vi ser, at der er tale om et minimumspunkt i \(t=t_0\).

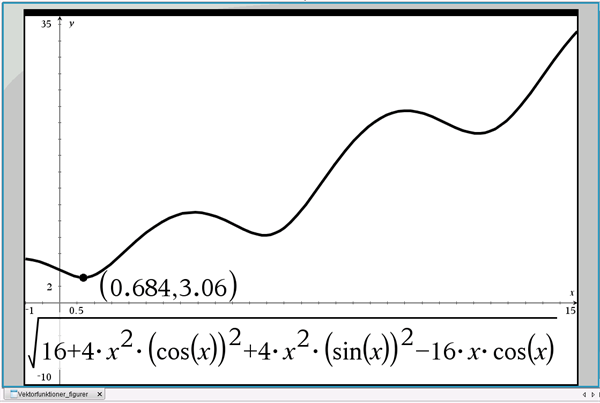
Figur 15    Afstanden fra punkt \(P(4,0)\) til punkter på Archimedes spiral som funktion af \(t\)