Koordinatsystemet i 3D

I rumgeometrien arbejder man med tredimensionelle koordinatsystemer. Hvor man i to dimensioner kun har to akser (x og y), har man i tre dimensioner tilføjet en ekstra akse, z-aksen.

Man kan sammenligne det med et værelse. I to dimensioner har vi en plantegning, hvor vi ser værelset oppefra. Vi kan se hvordan møblerne står på gulvet i forhold til hinanden. Men vi kan ikke se, hvor høje de er. I tre dimensioner har vi tilføjet højden, så vi udover at se, hvordan møblerne er placeret i forhold til hinanden også skelner mellem øverste og nederste hylde i reolen.

Man tegner typisk akserne, så x-aksen peger udad, y-aksen henad og z-aksen opad.

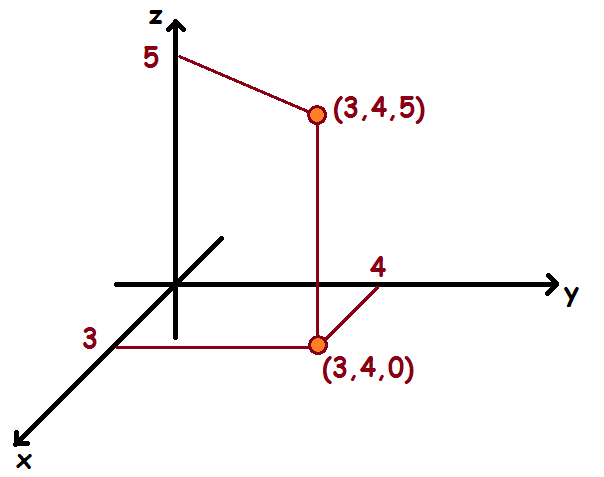
Man aflæser et punkts koordinater ved først at gå ud af x-aksen, indtil man er nået på linje med punktets x-værdi. Derefter går man parallelt med y-aksen, indtil man er nået på linje med punktet, og til sidst går man op parallelt med z-aksen, indtil man når på linje med punktet.

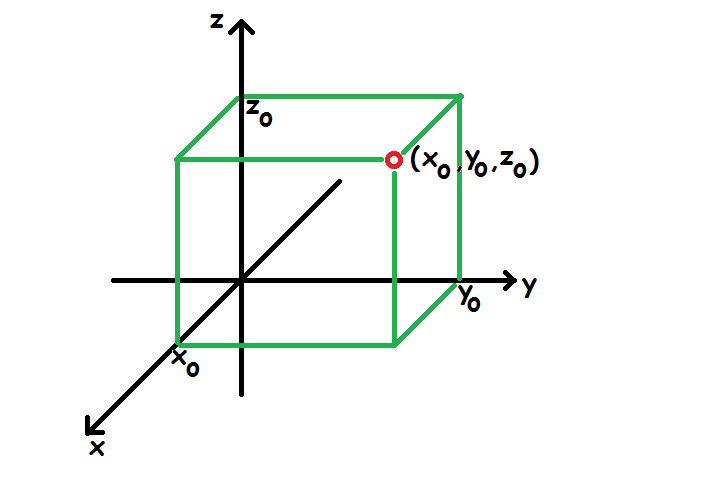
Hvis man skal afsætte et punkt i et tredimensionelt koordinatsystem, finder man punktet i xy-planen med de rigtige x- og y-værdier. Dette punkt har koordinaterne (x, y, 0). Herfra går man lodret op (eller ned) til man når den rigtige z-værdi. Herunder er punktet (3, 4, 5) indtegnet.