Tangentplan til kugle

Ligesom en cirkel i hvert punkt har en tangentlinje, så har en kugle i hvert punkt en tangentplan. En tangentplan er altså en plan, der rører kuglen i ét (og kun ét) punkt.

Man kan forestille sig tangentplanen som et stykke karton, der ligger op ad en fodbold.

I opgaver bliver man tit bedt om at bestemme en ligning for tangentplanen i et kendt punkt på kuglen.

Vi husker på, at man for at kunne opskrive en ligning for en plan skal kende et fast punkt i planen samt en normalvektor for planen. Som punktet, kan man bruge det punkt, man har fået opgivet, som altså ligger både på kuglen og i tangentplanen (røringspunktet). Så mangler man altså bare en normalvektor. Vektoren, der starter i det kendte punkt på kuglens overflade og slutter i centrum af kuglen vil være vinkelret på tangentplanen. Derfor kan vi bruge den som normalvektor.

Lad os se på et eksempel.

Vores kugle har ligningen

$$\mathcal{K}:\quad(x+2)^2+(y-1)^2+(z+1)^2=9$$

og punktet

$$P(-4,3,0)$$

ligger på kugleskallen (man kan tjekke efter, at P rent faktisk ligger på kugleskallen ved at indsætte det i kuglens ligning og se, om den er opfyldt).

Vi ønsker at bestemme en ligning for kuglens tangentplan i punktet P.

Vores faste punkt i planen er P.

Vores normalvektor er vektoren fra P til C.

Vi aflæser fra kuglens ligning, at centrum har koordinaterne C(-2,1,-1).

Nu udregner vi normalvektorens koordinater

$$\overrightarrow{n}=\overrightarrow{PC}=\begin{pmatrix}-2-(-4)\\1-3\\-1-0\end{pmatrix}=\begin{pmatrix}2\\-2\\-1\end{pmatrix}$$

Til sidst skal vi bare sætte ind i formlen for planens ligning.

$$a(x-x_0)+b(y-y_0)+c(z-z_0)=0$$

$$2(x-(-4))+(-2)(y-3)+(-1)(z-0)=0$$

$$2(x+4)-2(y-3)-z=0$$

$$2x+8-2y+6-z=0$$

$$2x-2y-z+14=0$$

Og dette er så ligningen for tangentplanen til kuglen i punktet P.

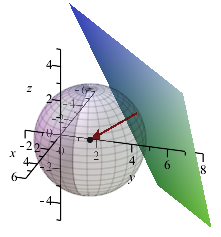
Nedenfor er indtegnet kuglen, planen og normalvektoren fra eksemplet ovenfor.