Overgangsformler

Der er en række formler for, hvordan man kan omskrive forskellige værdier af trigonometriske funktioner.

Vi begrunder dem alle sammen ved hjælp af en grafiske fremstilling.

De første overgangsformler er

$$\begin{align}
\cos(x+2\pi) &= \cos(x) \\[0.5em]
\sin(x+2\pi) &= \sin(x) \\[0.5em]
\tan(x+2\pi) &= \tan(x)
\end{align}$$

Disse formler skyldes, at når man lægger \(2\pi\) til en vinkel, så kører man en hel runde på cirklen. Man når altså tilbage til det samme sted, og derfor er cosinus- og sinus-værdierne de samme. Og da tangens er sinus divideret med cosinus, så er tangens-værdien også uændret.

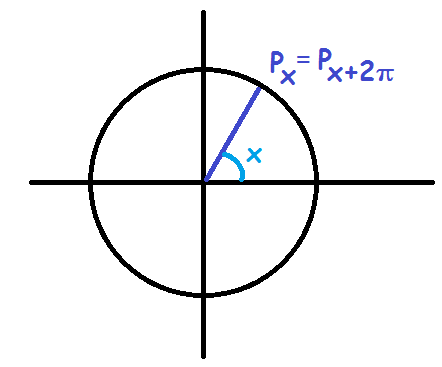
I de næste overgangsformler, vi skal se på, sammenligner vi vinkel \(x\) med vinkel \(-x\).

$$\begin{align}
\cos(-x) &= \cos(x) \\[0.5em]
\sin(-x) &= -\sin(x) \\[0.5em]
\tan(-x) &= -\tan(x)
\end{align}$$

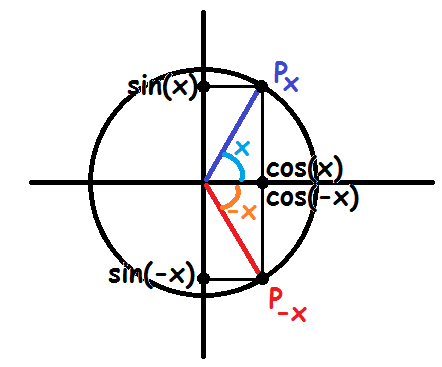
\(P_x\) og \(P_{-x}\) er spejlinger i \(x\)-aksen. Derfor er deres \(x\)-værdi den samme. Derfor er \(\cos(x)=\cos(-x)\).

Deres \(y\)-værdier har derimod skiftet fortegn. Derfor er \(\sin(-x)=-\sin(x)\)
Tangens-værdien får man ved at dividere de to med hinanden

$$\tan(-x)=\frac{\sin(-x)}{\cos(-x)}=\frac{-\sin(x)}{\cos(x)}=-\frac{\sin(x)}{\cos(x)}=-\tan(x)$$

Nu prøver vi at sammenligne vinklerne \(x\) og \(\tfrac{\pi}{2}-x\). (Vi husker på at \(\tfrac{\pi}{2}\) svarer til 90 grader).

Her er overgangsformlerne

$$\begin{align}
\cos\left(\frac{\pi}{2}-x\right) &= \sin(x) \\[0.5em]
\sin\left(\frac{\pi}{2}-x\right) &= \cos(x) \\[0.5em]
\tan\left(\frac{\pi}{2}-x\right) &= \frac{1}{\tan(x)}
\end{align}$$

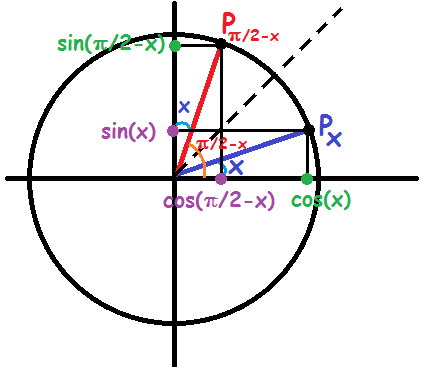
Punkterne \(P_x\) og \(P_{\tfrac{\pi}{2}-x}\) er spejlinger i linjen \(y=x\). Derfor svarer den enes \(x\)-værdi til den andens \(y\)-værdi.

Vi dividerer sinus med cosinus for at nå frem til tangens

$$\tan\left(\frac{\pi}{2}-x\right)=\frac{\sin(\frac{\pi}{2}-x)}{\cos(\frac{\pi}{2}-x)}=\frac{\cos(x)}{\sin(x)}=\frac{\cos(x)/\cos(x)}{\sin(x)/\cos(x)}=\frac{1}{\tan(x)}$$

Nu sammenligner vi vinklerne \(x\) og \(\pi-x\). (Vi husker på at \(\pi\) svarer til 180 grader).

Her er overgangsformlerne

$$\begin{align}
\cos(\pi-x) &= -\cos(x) \\[0.5em]
\sin(\pi-x) &= \sin(x) \\[0.5em]
\tan(\pi-x) &= -\tan(x)
\end{align}$$

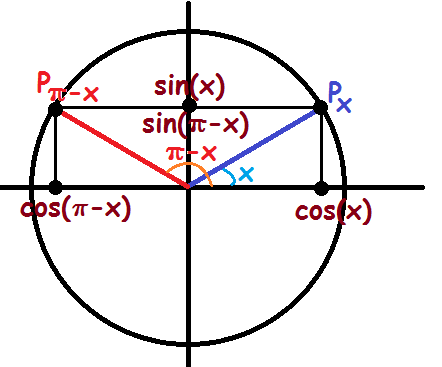
Punkterne \(P_x\) og \(P_{\pi-x}\) er spejlinger i \(y\)-aksen. Derfor er deres \(y\)-værdier (deres sinus-værdier) ens. Deres \(x\)-værdier (cosinus-værdierne) har derimod skiftet fortegn.

Vi udregner tangens:

$$\tan(\pi-x)=\frac{\sin(\pi-x)}{\cos(\pi-x)}=\frac{\sin(x)}{-\cos(x)}=-\frac{\sin(x)}{\cos(x)}=-\tan(x)$$

De sidste overgangsformler, vi skal se på, er mellem vinklerne \(x\) og \(\pi+x\)
I dette tilfælde er overgangsformlerne

$$\begin{align}
\cos(\pi+x) &= -\cos(x) \\[0.5em]
\sin(\pi+x) &= -\sin(x) \\[0.5em]
\tan(\pi+x) &= \tan(x)
\end{align}$$

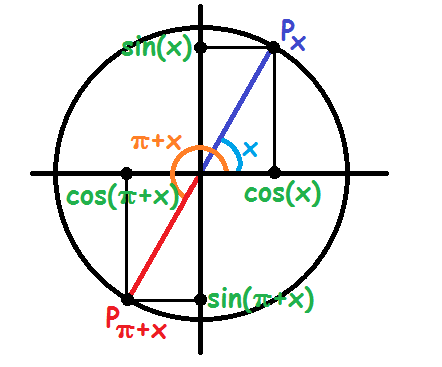
Vi kan se, at punkternes \(x\)-koordinater er ens bortset fra et modsat fortegn. Det samme gælder \(y\)-koordinaterne.

$$\tan(\pi+x)=\frac{\sin(\pi+x)}{\cos(\pi+x)}=\frac{-\sin(x)}{-\cos(x)}=\frac{\sin(x)}{\cos(x)}=\tan(x)$$

Opsamling

For lige at samle op skriver vi her alle overgangsformlerne op

$$\begin{align}
\cos(x+2\pi) &= \cos(x) \\[0.5em]
\cos(-x) &= \cos(x) \\[0.5em]
\cos\left(\frac{\pi}{2}-x\right) &= \sin(x) \\[0.5em]
\cos(\pi-x) &= -\cos(x) \\[0.5em]
\cos(\pi+x) &= -\cos(x) \\[0.5em]
\sin(x+2\pi) &= \sin(x) \\[0.5em]
\sin(-x) &= -\sin(x) \\[0.5em]
\sin\left(\frac{\pi}{2}-x\right) &= \cos(x) \\[0.5em]
\sin(\pi-x) &= \sin(x) \\[0.5em]
\sin(\pi+x) &= -\sin(x) \\[0.5em]
\tan(x+2\pi) &= \tan(x) \\[0.5em]
\tan(-x) &= -\tan(x) \\[0.5em]
\tan\left(\frac{\pi}{2}-x\right) &= \frac{1}{\tan(x)} \\[0.5em]
\tan(\pi-x) &= -\tan(x) \\[0.5em]
\tan(\pi+x) &= \tan(x)
\end{align}$$