Afstand mellem punkt og plan

Hvis man har oplyst et punkt P₁(x₁, y₁, z₁) og et plan α: ax+by+cz+d=0, så er afstanden mellem dem givet ved formlen

$$\text{dist}(\alpha,P_1)=\frac{|ax_1+by_1+cz_1+d|}{\sqrt{a^2+b^2+c^2}}$$

Den afstand, man måler, er den vinkelrette afstand mellem punktet og planen.

 

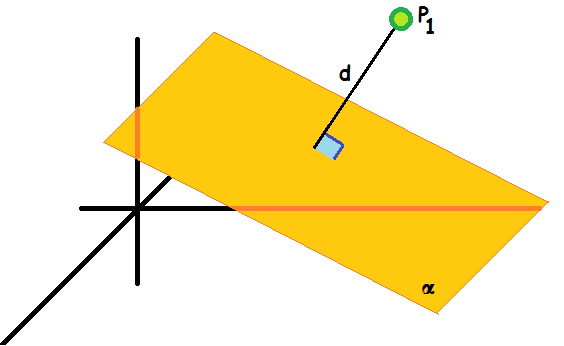
Læg mærke til, hvordan formlen minder om afstanden mellem en linje og et punkt i 2D.

Lad os se, hvordan formlen virker ved hjælp af et eksempel.

$$\alpha:\:2x+y-2z-14=0$$

$$P_1(-1,-1,2)$$

Altså er a=2, b=1, c= -2, d= -14, x₁= -1, y₁= -1, og z₁=2.

Nu sætter vi ind i formlen

$$\text{dist}(\alpha,P_1)=\frac{|2\cdot(-1)+1\cdot(-1)-2\cdot(2)-14|}{\sqrt{2^2+1^2+(-2)^2}}=\frac{|-2-1- 4-14|}{\sqrt{4+1+4}}$$

$$=\frac{|-21|}{\sqrt{9}}=\frac{21}{3}=7$$

Altså er den korteste (den vinkelrette) afstand mellem punktet og planen 7 længdeenheder.

Hvis man får afstanden mellem et punkt og et plan til at være 0, så betyder det, at punktet ligger i planen.

Hvad hvis planen er givet ved parameterfremstilling?

Hvis planen er givet ved parameterfremstilling, omregner man den til en ligning.

Man kender allerede et fast punkt, og man kan udregne en normalvektor ved at krydse de to retningsvektorer med hinanden.

Når man har omregnet planen fra parameterfremstilling til ligning, kan man bruge formlen ovenfor.