Lodret og vandret tangent for en vektorfunktion

Fra forrige afsnit ved vi, at tangentvektoren til en vektorfunktion er givet ved:

\(\overrightarrow{v(t)}=(x’(t), y’(t))\)

For at undersøge om kurven for en vektorfunktion indeholder vandret eller lodret tangent, skal vi søge løsninger til de to ligninger:

Vandret tangent:                          \(y’(t)=0\)

Lodret tangent:                            \(x’(t)=0\)

Eksempel

Vi vender tilbage til spiralen fra afsnit 2, se figur 13. Her er:
\(x(t)=5+t\cdot\cos(t)\) og \(y(t)=5-t\cdot\sin(t)\), hvor \(t\geq0\).

Vandret tangent:
\(y’(t)=-\sin(t)-t\cdot\cos(t)=0\) og dermed \(\tan(t)=-t\),
hvor de tre første løsninger er \(t=0, t=2,03\) og \(t=4,91\).

Lodret tangent:
\(x’(t)=\cos(t)-t\cdot\sin(t)=0\) og dermed \(\tan(t)=\dfrac{1}{t}\), hvor de tre første løsninger er \(t=0,86, t=3,43\) og \(t=6,44\).

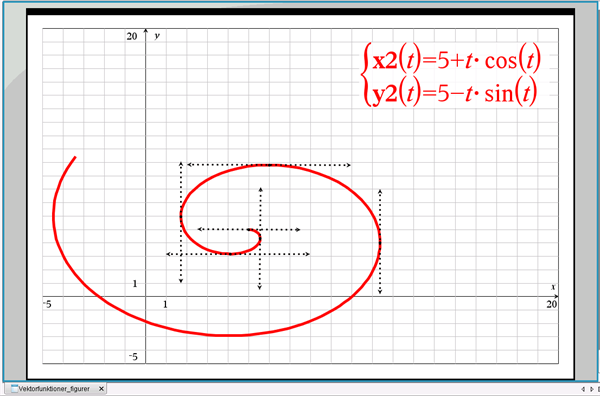
Figur 13 Spiralen fra afsnit 2, her gengivet med de tre første vandrette og lodrette tangenter indtegnet 

Punkter på spiralen med hhv. vandret og lodret tangent:
\begin{matrix}
t & x & y &     & t & x & y \\
0,0 & 5,0 & 5,0 &     & 0,86 & 5,6 & 4,3 \\
2,03 & 4,1 & 3,2 &     & 3,43 & 1,7 & 6,0 \\
4,91 & 6,0 & 9,8 &     & 6,44 & 11,4 & 4,0
\end{matrix}