Planens parameterfremstilling

Ligesom linjen har en parameterfremstilling, så kan man også lave en parameterfremstilling for planen. Det kræver, at man kender ét punkt i planen og to ikke-parallelle vektorer, der ligger i planen.

Parameterfremstillingen for planen ser således ud:

$$\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}x_0\\y_0\\z_0\end{pmatrix}+s\cdot\begin{pmatrix}p_1\\p_2\\p_3\end{pmatrix}+t\cdot\begin{pmatrix}q_1\\q_2\\q_3\end{pmatrix}$$

eller skrevet kortere

$$\overrightarrow{OP}=\overrightarrow{OP_0}+s\cdot\overrightarrow{p}+t\cdot\overrightarrow{q}$$

Vektorerne p og q kaldes retningsvektorer for planen.

Planens parameterfremstilling fungerer på den måde, at man kan nå ud til alle punkter i planen ved at starte i P₀ og derfra gå først et stykke parallelt med den ene vektor og dernæst et stykke parallelt med den anden. Nedenfor er tegnet, hvor man går 3 af den ene vektor og 2 af den anden ud fra punktet for at nå frem til det orange punkt.

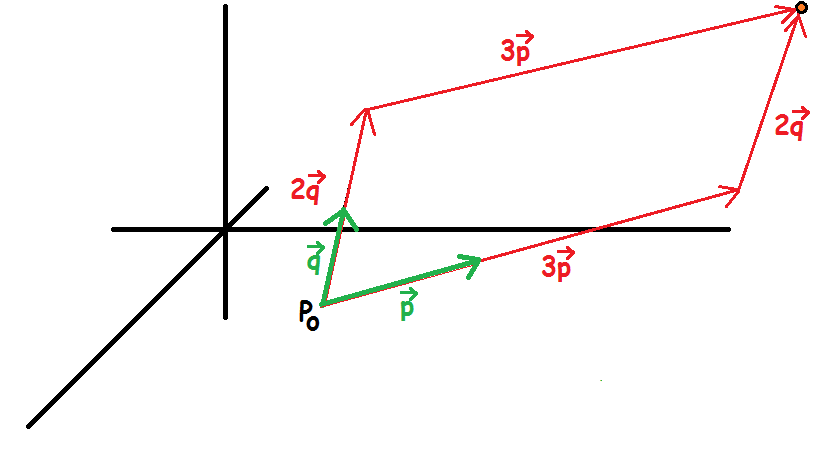
Ved at sætte forskellige tal ind på s's og t's plads kan man nå ud til alle punkter i planen.

Finde ligning når man kender parameterfremstilling

Hvis man kender parameterfremstillingen for et plan, kan man let finde dens ligning. Man finder normalvektoren ved at krydse de to retningsvektorer med hinanden

$$\overrightarrow{n}=\overrightarrow{p}\times\overrightarrow{q}$$

og man kender allerede et punkt i planen. Så kender man alt, hvad man har brug for for at kunne opskrive en ligning for planen

Finde parameterfremstilling, hvis man kender ligning

Hvis man kender ligningen for et plan, kan man gå den anden vej og finde en parameterfremstilling for planen.

Vi illustrerer metoden med et eksempel.

$$\alpha:\quad 2x+4y-6z-1=0$$

Først isolerer man den ene variable. Man bestemmer selv hvilken. Vi vælger at isolere x.

$$x=\frac{1}{2}-2y+3z$$

Nu lader man de to andre variable være parametrene. Vi sætter y=s og z=t.
Dermed har vi de tre ligninger

$$x=\frac{1}{2}-2s+3t$$

$$y=s$$

$$z=t$$

Vi kan også skrive det som

$$x=\frac{1}{2}-2\cdot s+3\cdot t$$

$$y=0+1\cdot s+0\cdot t$$

$$z=0+0\cdot s+1\cdot t$$

og dette kan på vektorform skrives som

$$\begin{pmatrix} x\\y\\z \end{pmatrix}=\begin{pmatrix} \frac{1}{2}\\ 0\\0 \end{pmatrix}+s\cdot\begin{pmatrix} -2\\1\\0 \end{pmatrix}+t\cdot\begin{pmatrix} 3\\0\\1 \end{pmatrix}$$

hvorved vi er nået frem til en parameterfremstilling for planen.