Avancerede emner indenfor Multipel regression

Disse emner falder udenfor pensum men for den nysgerrige er her en kort introduktion til emner, som er vigtige i forbindelse med regressionsanalyse.

Udforskende dataanalyse

Indenfor området data science arbejder man en del med udforskende dataanalyse. Dette indebærer, at man før man kaster sig hovedkuls ud i at vælge den ene eller anden model, så tager man sig tid til at undersøge data nærmere. Det giver fx ikke mening at bruge en lineær regressionsmodel, hvis man på en graf kan se, at der umuligt kan være en lineær sammenhæng mellem en afhængig variable og en forklarende variabel. Det er ikke helt nemt at afgøre, om der kan være en lineær sammenhæng mellem en afhængig variable og flere forklarende variable. Så på nuværende tidspunkt er det bedste man kan gøre, at undersøge om det er plausibelt, at der er en lineær sammenhæng mellem ens afhængige variabel og de forklarende variable en for en.

Der findes et klassisk eksempel under navnet Anscombes kvartet, hvor statistikeren Francis Anscombe viser fire forskellige datasæt med næsten identiske deskriptive statistikker (som fx middelværdi og varians), men når man laver en graf for hver af datasættene, så får man meget forskellige grafer.

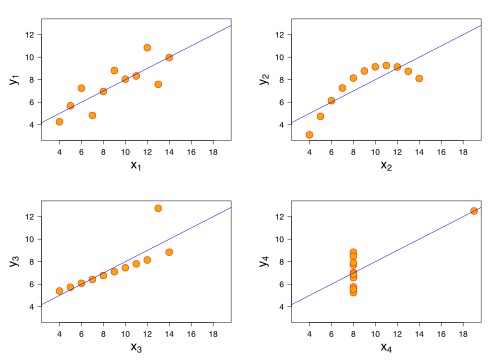
Grafen er fra "Anscombe's quartet 3.svg. (2016, December 14). Wikimedia Commons, the free media repository'', hvor den original fil findes her.

Model udvælgelse og multicollinearitet

Lad os sige, at vi har en model med en afhængig variabel og fire forklarende variable.
\(
y = b_0 + b_1 x_2 + b_2 x_2 + b_3 x_3 + b_4 x_4
\)
Hvordan kan vi være sikre på, at dette er den rigtige model. Måske skulle vi hellere udelade \(x_2\) eller \(x_3\) eller både \(x_2\) og \(x_3\). Sådanne spørgsmål forsøger man at besvare indenfor emnet model udvælgelse. Der findes en række statistiske tests, som kan være med til at afgøre, om det er en god ide eller ej at inkludere de enkelte variable.

Når man vælger de forklarende variable skal man også passe på med multicollinearitet. Derfor må ingen af de forklarende variable kunne skrives som lineære funktioner af de øvrige forklarende variable. I eksempel med fire forklarende variable kan vi fx ikke have at
\(
x_2 = x_1 + x_4
\)

Justeret \(R^2\)

I forlængelse af forrige afsnit om model udvælgelse er det værd at bemærke følgende. Hvis vi tilføjer flere forklarende variable til vores model, så vil det stort set næsten altid være sådan, at værdien af \(R^2\) bliver større. Betyder det, at det altid er godt at tilføje flere forklarende variable til ens model? Hvis vi har \(n\) observationer, så kan vi jo vælge en model med \(n-1\) forklarende variable. Dette vil ofte give en værdi af \(R^2\) meget tæt på 1. Så må det jo være en god model! Svaret er nej. Derfor bruger man ofte ikke determinationskoefficienten \(R^2\) men en værdi, som kaldes justeret \(R^2\), når man skal se på om det giver mening at tilføje en ekstra variable til modellen.

Korrelation og kausalitet

Når vi arbejder med lineær regressionsanalyse, leder vi efter korrelationer mellem den afhængige variable og en række forklarende variable. Det er meget vigtigt at have for øje, at en lineær sammenhæng mellem en række variable ikke er ensbetydende med en kausalitet eller årsagssammenhæng mellem de samme variable. På videnskab.dk kan du finde en let tilgængelig artikel om korrelation og kausalitet og lære mere om forskellen samt hvad man skal passe på med.