Parameterfremstillingen for en cirkel
Vi forestiller os en partikel, der gennemløber en cirkulær bevægelse med radius \(r\) og vinkelhastighed \(\omega\) (rad/sek., positiv omdrejningsretning, dvs. mod uret). Tiden for ét gennemløb af cirklen betegnes partiklens omløbstid og er \(T=\frac{2\pi}{\omega}\).
Vi afbilder bevægelsen i et koordinatsystem som cirklen med centrum i (0,0) og radius \(r\), se figur 6. Ethvert punkt på cirkelperiferien kan beskrives ved stedvektoren:
\(\overrightarrow{r(t)}=(x(t),y(t))=(r\cdot \cos(\omega t), r\cdot \sin(\omega t))\), \(0\leq t\leq \frac{2\pi}{\omega}\)
(hvor definitionsmængden for \(t\) her er afgrænset svarende til ét fuldt gennemløb af cirklen, men definitionsmængden for \(t\) kunne være opadtil ubegrænset svarende til uendeligt mange gennemløb af cirklen.)
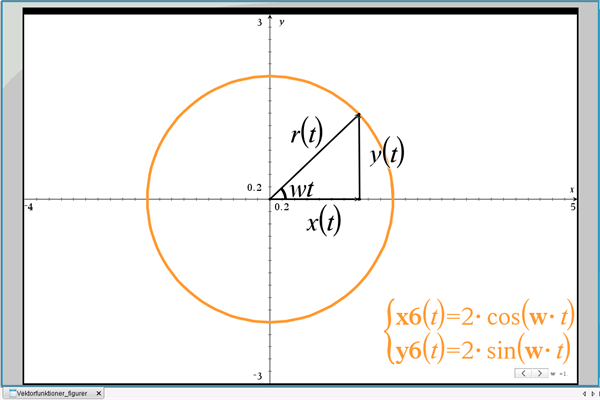
Figur 6 Parameterfremstilling for en cirkel
