Vektorfunktioner
Du er vant til at arbejde med funktioner (og deres grafer) i et koordinatsystem, hvor y-værdien (den afhængige variabel) er beskrevet som en funktion af x (den uafhængige variabel). Det kunne eksempelvis være \(y(x)=2x^2+4x-16\), der er et andengradspolynomium, hvor grafen er en parabel, se figur 1.
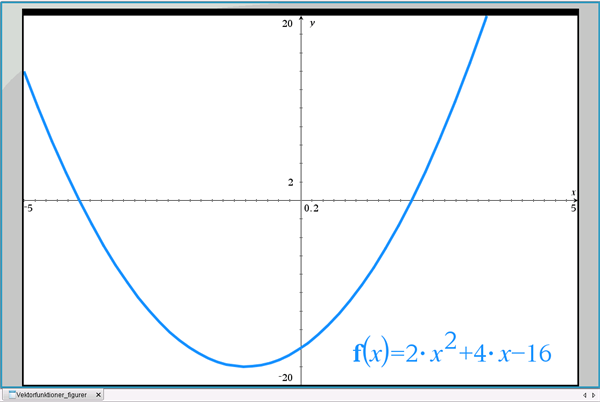
Figur 1 Parablen \(y(x)=2x^2+4x-16\)
Når vi ser på funktioner og deres grafer, er det en forudsætning, at der er éntydighed, hvad angår funktionsværdier. Det betyder, at der for en hvilken som helst x-værdi i definitionsmængden skal være én og kun én tilhørende y-værdi. Dette er opfyldt for parablen i figur 1.
Men hvis du forestiller dig en liggende parabel, se figur 2, er denne betingelse ikke opfyldt. For alle x-værdier til højre for parablens toppunkt er der to tilhørende y-værdier. Vi vil vende tilbage til dette eksempel senere.
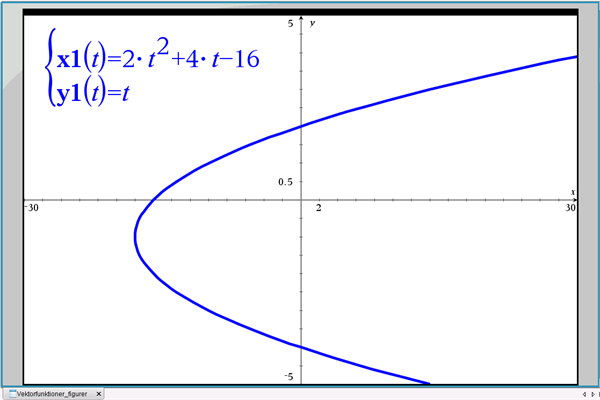
Figur 2 Liggende parabel.
