Kontinuitet og differentiabilitet
Kontinuitet og differentiabilitet er to vigtige begreber indenfor matematisk analyse. Det er begreber, der omhandler egenskaber ved funktioner.
Vi skal huske på, at en funktion bare er en ordning, der til hver x-værdi i definitionsmængden knytter én og kun én y-værdi.
Følgende grafer er grafer for funktioner.
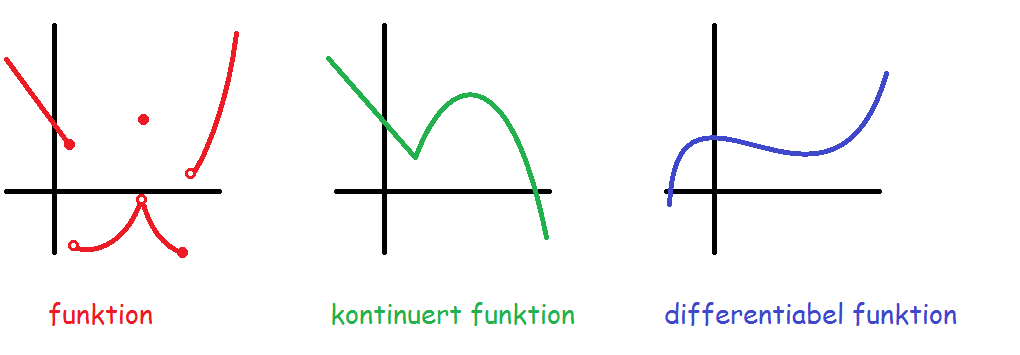
Den første graf er godt nok en funktion (for hver x-værdi er der netop én y-værdi), men den er ikke særligt pæn at regne på. Den hopper og springer.
Den anden funktion er noget pænere. Den er nemlig sammenhængende. Vi kan tegne den uden at løfte blyanten fra papiret. Den type af funktioner kaldes kontinuerte (IKKE kontinuerlige!)
Den tredje graf viser en funktion, der både er sammenhængende og som desuden er "glat". Dvs. at den ikke har nogen "knæk". Den type af funktioner kaldes differentiable.
At en funktion er differentiabel betyder også, at man kan tegne en entydig tangent i hvert eneste punkt på grafen. Det kan man ikke, hvis der er et knæk. I knækpunkter kan man tegne to tangenter, og det bliver noget rod.
Nedenfor er tegnet en funktionsgraf (grøn) med et knæk. I knækket kan man tegne tangenten fra venstre og tangenten fra højre.
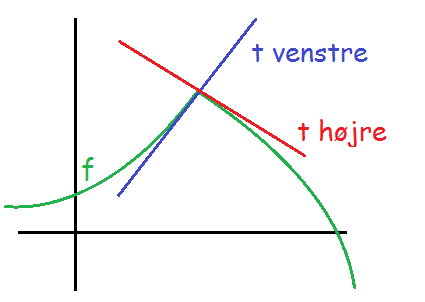
Det er kun de differentiable funktioner, man kan differentiere.
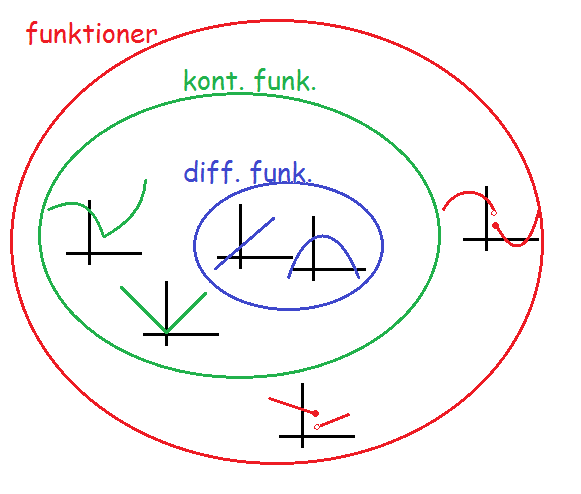
Alle de differentiable funktioner er også kontinuerte (fordi de er sammenhængende). Derved kan man sige, at differentiabilitet er en "finere" egenskab end kontinuitet.
Man kan tegne det som følgende diagram. Den røde cirkel er mængden af alle funktioner. Inde i den ligger delmængden af kontinuerte funktioner (de sammenhængende) (grøn cirkel). Inde i de kontinuerte funktioner ligger delmængden af differentiable funktioner (sammenhængende og glatte) (den blå cirkel).