Vinkel mellem linje og plan

Hvis man har en linje og et plan, vil de skære hinanden i et punkt (medmindre de er parallelle), og der vil dannes en vinkel imellem dem.

Denne vinkel kan vi beregne.

Først finder man vinklen mellem planens normalvektor og linjens retningsvektor.

Dette gør man med den formel, vi kender fra 2D

$$\cos(u)=\frac{\overrightarrow{n}\cdot \overrightarrow{r}}{|\overrightarrow{n}|\cdot|\overrightarrow{r}|}$$

Hvis vi trækker denne vinkel fra 90º får vi vinklen mellem linjen og planen

$$v=90^\circ-u$$

Det kan illustreres med følgende tegning

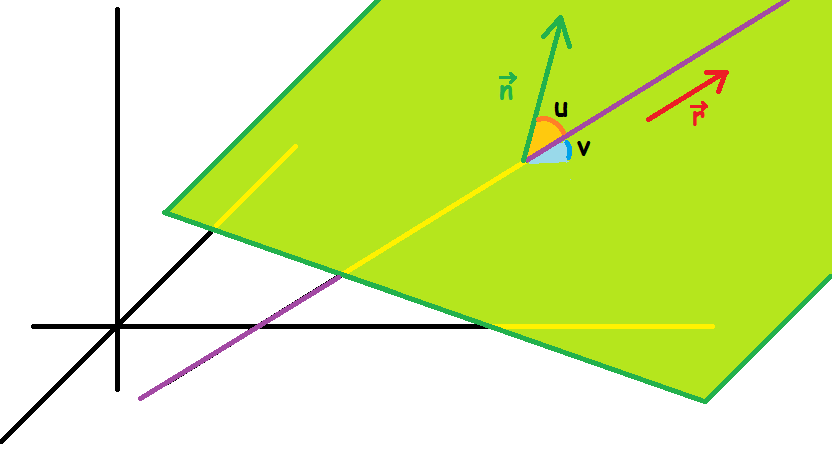
Der findes et lille trick man kan bruge, for at spare lidt tid. Sinus og cosinus er komplimentære funktioner, derfor gælder følgende

$$\sin(\theta)=\cos(90^\circ-\theta)$$

Vi viste før hvordan vi fandt vinklen v, nemlig ved at trække vinklen u fra 90 grader, hvilket minder meget om ovenstående ligning. Derfor kan man gøre følgende

$$\sin(v)=\cos(u)=\frac{\overrightarrow{n}\cdot \overrightarrow{r}}{|\overrightarrow{n}|\cdot|\overrightarrow{r}|}$$

Man kan med fordel bruge sinus, og dermed spare sig selv en beregning, men det er ikke forkert at bruge cosinus og derefter bestemme v, som det er vist ovenfor.