Archimedes' spiral

Parameterfremstillingen for Archimedes’ spiral, opkaldt efter den græske matematiker Archimedes, er (\(t\) angiver radianer):

\(\overrightarrow{r(t)}=(x(t), y(t)) = a\cdot (t\cdot\cos(t), t\cdot\sin(t))\), \(0 \leq t < +\infty\)

Kurven er en spiral, der starter i (0,0) og har positiv omløbs­retning mod uret, se figur 11, hvor vi har sat \(a=2\).

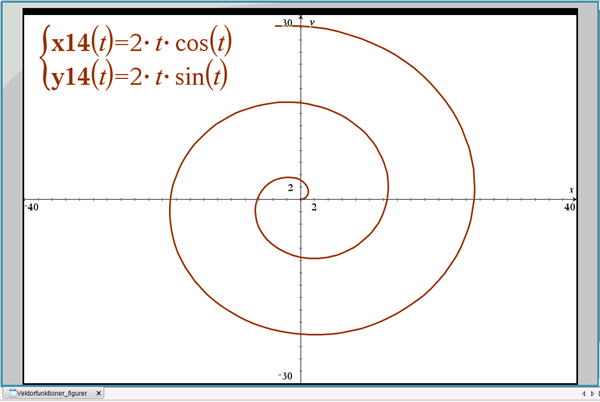
Figur 11    Archimedes spiral

Skæring med y-aksen:

For at finde skæringspunkter med y-aksen skal vi søge løsninger til ligningen \(x(t)=0\), dvs.:

\(t\cdot\cos(t)=0\), med løsningerne: \(t=0\) og \(t=n\cdot\pi+\frac{\pi}{2}\), hvor \(n=1, 2, 3 ...\)

Skæring med x-aksen:

For at finde skæringspunkter med x-aksen skal vi søge løsninger til ligningen \(y(t)=0\), dvs.:

\(t\cdot\sin(t)=0\), med løsningerne: \(t=0\) og \(t=n\cdot\pi\), hvor \(n=1, 2, 3 ...\)

Ved at indsætte disse løsninger i vektorfunktionen ser vi, at afstanden (målt på akserne) mellem to på hinanden følg­ende skæringspunkter med enten y-aksen eller x-aksen er den samme for alle skæringspunkter, nemlig \(a\cdot\pi\).

Vi formulerer det som, at Archimedes spiral skærer akserne i uendelig mange punkter med ækvidistant afstand \(a\cdot\pi\).