Skæring mellem planer

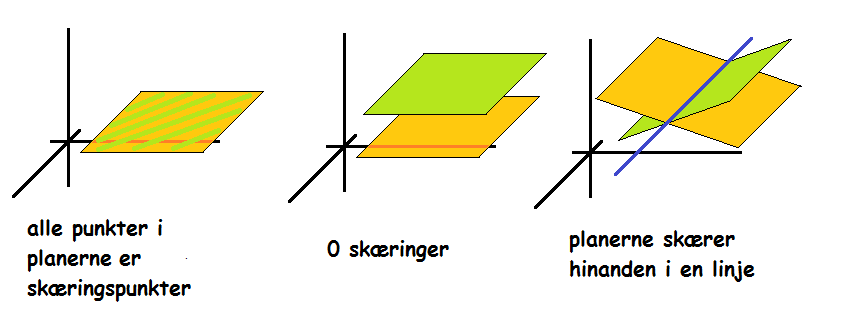
Hvis man har to planer, kan de ligge på tre forskellige måder i forhold til hinanden.

• Hvis de to planer er ens (deres normalvektorer er parallelle, og de har et fælles punkt), så skærer de hinanden over hele planen.

• Hvis de to planer er parallelle (deres normalvektorer er parallelle, men de har ingen fælles punkter), så skærer de to planer ikke hinanden.

• Hvis de to planers normalvektorer ikke er parallelle, vil planerne skære hinanden i en linje.

Man starter med at undersøge om planerne er parallelle. Det gør man ved at undersøge om deres normalvektorer er parallelle. Man krydser de to normalvektorer med hinanden. Hvis krydsproduktet giver nulvektoren, er de parallelle. (Hvis den ene (eller begge) planer er givet ved parameterfremstilling, finder man planens normalvektor ved at krydse dens to retningsvektorer med hinanden).

Hvis planerne er parallelle, undersøger man om de er sammenfaldende eller ej. Man undersøger om det faste punkt fra den ene plan ligger i den anden ved at indsætte i dens ligning. (Hvis en eller begge planer er givet ved parameterfremstilling kan man tage det faste punkt fra den ene og indsætte på venstresiden af den anden. Så løser man to af ligningerne med to ubekendte. De fundne parameterværdier indsættes så i den tredje ligning. Hvis den er opfyldt, ligger punktet i begge planer).

Hvis planerne ikke er parallelle, skærer de hinanden i en linje. Vi beviser først, at krydsproduktet af de to planers normalvektorer udgør en retningsvektor for skæringslinjen.

Bevis for skæringslinjens retningsvektor

Antag, at vi kender et punkt \(P(x_0, y_0, z_0)\), som ligger på skæringslinjen mellem to planer med ligningerne hhv. \(\alpha: a_1\cdot x + a_2\cdot y + a_3\cdot z + k_\alpha = 0\) og \(\beta: b_1\cdot x + b_2\cdot y + b_3\cdot z + k_\beta = 0\).

En normalvektorer til hver af planerne er da:

$$\overrightarrow{n}_\alpha=\begin{pmatrix}a_1\\a_2\\a_3\end{pmatrix},\qquad\overrightarrow{n}_\beta=\begin{pmatrix}b_1\\b_2\\b_3\end{pmatrix}$$

og krydsproduktet mellem normalvektorerne er en vektor, \(\overrightarrow{r}\):

$$\overrightarrow{r} = \overrightarrow{n}_\alpha \times \overrightarrow{n}_\beta = \begin{pmatrix}a_2\cdot b_3 – a_3\cdot b_2\\a_3\cdot b_1 – a_1\cdot b_3\\a_1\cdot b_2 – a_2\cdot b_1\end{pmatrix}$$

Vi betragter en linje \(l\), som inkluderer punkt \(P\) og har \(\overrightarrow{r}\)  som retningsvektor. Denne linje kan beskrives ved parameterfremstillingen:

\(l: (x, y, z) = (x_0, y_0, z_0) + t\cdot \overrightarrow{r}\), hvor \(–\infty < t < +\infty\)

Vi indsætter nu parameterfremstillingen for linjen \(l\) i ligningerne for de to planer, idet vi i sidste linje af udregningerne for hver plan udnytter, at koordinatsættet til punkt \(P\) opfylder planens ligning:

Planen \(\alpha\): 

\(a_1\cdot (x_0 + t\cdot (a_2\cdot b_3 – a_3\cdot b_2)) + a_2\cdot (y_0 + t\cdot (a_3\cdot b_1 – a_1\cdot b_3))\) 
\(+\: a_3\cdot (z_0 + t\cdot (a_1\cdot b_2 – a_2\cdot b_1)) + k_\alpha\)
\(= (a_1x_0 + a_2y_0 + a_3z_0 + k_\alpha)\) 
\(+\: t\cdot (a_1a_2b_3 – a_1a_3b_2 + a_2a_3b_1 – a_2a_1b_3 + a_3a_1b_2 – a_3a_2b_1)\)
\(= (a_1x_0 + a_2y_0 + a_3z_0 + k_\alpha) + t\cdot 0 = 0\)

Planen \(\beta\): 

\(b_1\cdot (x_0 + t\cdot (a_2\cdot b_3 – a_3\cdot b_2)) + b_2\cdot (y_0 + t\cdot (a_3\cdot b_1 – a_1\cdot b_3))\)
\(+\: b_3\cdot (z_0 + t\cdot (a_1\cdot b_2 – a_2\cdot b_1)) + k_\beta\)
\(= (b_1x_0 + b_2y_0 + b_3z_0 + k_\beta)\)
\(+\: t\cdot (b_1a_2b_3 – b_1a_3b_2 + b_2a_3b_1 – b_2a_1b_3 + b_3a_1b_2 – b_3a_2b_1)\)
\(= (b_1x_0 + b_2y_0 + b_3z_0 + k_\beta) + t\cdot 0 = 0\)

Parameterfremstillingen for linjen \(l\) ses at opfylde begge planers ligning, og vi har hermed bevist, at vektoren \(\overrightarrow{r} = \overrightarrow{n}_\alpha \times \overrightarrow{n}_\beta\) er retningsvektor for skæringslinjen mellem de to planer.

Lad os herefter se på, hvordan vi i praksis bestemmer en parameterfremstilling for skæringslinjen.

Begge planer er givet ved ligninger

Hvis begge planer er givet ved ligninger, finder man skæringslinjen ved følgende fremgangsmåde. Først krydser man de to normalvektorer med hinanden. Deres krydsprodukt er retningsvektoren for skæringslinjen. Dernæst skal man finde et punkt på linjen. Det gør man ved at sætte et fast tal ind i stedet for en af de variable (typisk z=0) og løse de to ligninger med to ubekendte. Derved vil man opnå et punkt der ligger på skæringslinjen. 

Nu kan man sammensætte det i en parameterfremstilling

Lad os illustrere med et eksempel.

$$\alpha:\quad x-3y+z-1=0$$

$$\beta:\quad 2x-5y-2z+4=0$$

Vi aflæser normalvektorerne ud fra ligningerne

$$\overrightarrow{n}_\alpha=\begin{pmatrix}1\\-3\\1\end{pmatrix},\qquad\overrightarrow{n}_\beta=\begin{pmatrix}2\\-5\\-2\end{pmatrix}$$

Skæringslinjens retningsvektor er krydsproduktet af de to normalvektorer

$$\overrightarrow{r}=\overrightarrow{n}_\alpha\times\overrightarrow{n}_\beta=\begin{pmatrix}&1\\&-3\\&1&\end{pmatrix}\times\begin{pmatrix}&2\\&-5\\&-2&\end{pmatrix}=$$

$$=\begin{pmatrix}&\begin{vmatrix}&-3 & &-5 \\&1 & & -2&\end{vmatrix}\\&-\begin{vmatrix}&1& &2 \\&1& & -2&\end{vmatrix}\\&\begin{vmatrix}&1& &2 \\&-3& &-5&\end{vmatrix}&\end{pmatrix}=$$

$$=\begin{pmatrix}&11\\&4\\&1&\end{pmatrix}$$

 Nu sætter vi z=0 i de to ligninger

$$x-3y+0-1=0$$

$$2x-5y-2\cdot0+4=0$$

Vi løser de to ligninger med to ubekendte ved substitutionsmetoden

$$x-3y-1=0\Leftrightarrow {\color{Red} x}=3y+1$$

$$2({\color{Red} {3y+1}})-5y+4=0\Leftrightarrow 6y+2-5y+4=0\Leftrightarrow y+6=0\Leftrightarrow {\color{Blue} y}=-6$$

$$x=3\cdot({\color{Blue} {-6}})+1=-18+1=-17$$

Nu har vi punktet (-17, -6, 0) som ligger på skæringslinjen.

Skæringslinjen har derfor parameterfremstillingen

$$l:\quad\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}-17\\-6\\0\end{pmatrix}+t\cdot\begin{pmatrix}11\\4\\1\end{pmatrix}$$

Et plan er givet ved ligningen, den anden ved parameterfremstilling

Hvis den ene plan er givet ved ligning og den anden ved parameterfremstilling, så finder man skæringslinjen på følgende måde.

Først indsætter man hver enkelt koordinatfunktion fra parameterfremstillingen i den anden plans ligning. Dernæst isolerer man den ene parameter. Dette indsætter man så igen i parameterfremstillingen, hvorved man kan reducere til linjens parameterfremstilling.

Lad os se på et eksempel:

$$\alpha:\quad2x-y+3z=0$$

$$\beta:\quad\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}1\\1\\0\end{pmatrix}+s\cdot\begin{pmatrix}2\\0\\1\end{pmatrix}+t\cdot\begin{pmatrix}-1\\3\\2\end{pmatrix}$$

Vi kan omskrive parameterfremstillingen til de tre koordinatfunktioner

$$x=1+2s-t$$

$$y=1+3t$$

$$z=s+2t$$

Disse indsætter vi nu i ligningen og isolerer den ene parameter

$$2(1+2s-t)-(1+3t)+3(s+2t)=0$$

$$2+4s-2t-1-3t+3s+6t=0$$

$$1+7s+t=0$$

$$t=-1-7s$$

Nu indsætter vi dette på t's plads i de tre koordinatfunktioner

$$x=1+2s-(-1-7s)=1+2s+1+7s=2+9s$$

$$y=1+3(-1-7s)=1-3-21s=-2-21s$$

$$z=s+2(-1-7s)=s-2-14s=-2-13s$$

Vi kan nu skrive det om til en parameterfremstilling

$$\begin{pmatrix}x\\y\\z\end{pmatrix}=\begin{pmatrix}2\\-2\\-2\end{pmatrix}+s\cdot\begin{pmatrix}9\\-21\\-13\end{pmatrix}$$

Begge planer er givet ved parameterfremstillinger

Hvis begge planer er givet ved parameterfremstillinger vil vi anbefale, at man omskriver den ene til en ligning (man kender allerede et fast punkt, og som normalvektor kan man bruge krydsproduktet af de to retningsvektorer. Læs evt. mere her). Nu har man den ene plan som ligning og den anden som parameterfremstilling, og man kan således bruge metoden ovenfor.

Der findes også en metode, hvor man ikke behøver omskrive til ligning, men den er relativt indviklet, så den vil vi forbigå her.