Længde og afstandsformlen

Man betegner længden af en vektor som

$$|\overrightarrow{a}|$$

Man finder længden af en vektor ved følgende formel

$$|\overrightarrow{a}|=\sqrt{a_1^2+a_2^2}$$

Formlen er let at udlede ved hjælp af Pythagoras' læresætning.

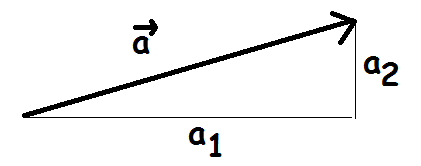
Vi har en retvinklet trekant.

$$|a_1|^2+|a_2|^2=|\overrightarrow{a}|^2$$

Bemærk at stregerne omkring a₁ og a₂ betyder "numerisk værdi", mens stregerne omkring vektor a betyder "længde". Dette skyldes at a₁ og a₂ bare er tal, mens vektor a er en vektor. Hvis man tager numerisk værdi af et tal og sætter det i anden, så får man det samme som hvis man bare havde sat tallet selv i anden (fordi minus gange minus giver plus, og plus gange plus giver plus). Derfor kan vi omskrive til:

$$a_1^2+a_2^2=|\overrightarrow{a}|^2$$

Nu er der bare tilbage at tage kvadratroden på begge sider, så har man formlen for længden af en vektor.

Hvis man f.eks. vil finde længden af vektoren

$$\overrightarrow{a}=\begin{pmatrix}3\\4\end{pmatrix}$$

så er den

$$|\overrightarrow{a}|=\left|\begin{pmatrix}3\\4\end{pmatrix}\right|=\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5$$

Afstandsformlen

Når man vil bestemme afstanden mellem to punkter, så er det det samme som at finde længden af vektoren mellem de to punkter. Altså kan man sige, at

$$|AB|=|\overrightarrow{AB}|$$

Her betyder venstresiden "længden af linjestykket mellem A og B" og højresiden betyder "længden af vektor AB".

For at finde afstanden mellem to punkter kan vi altså bruge formlen for længden af en vektor, hvor vi indsætter koordinaterne for vektor AB.

$$|AB|=\sqrt{(b_1-a_1)^2+(b_2-a_2)^2}$$

Hvis man f.eks. vil finde afstanden mellem punkterne (1, 2) og (5,3) er den

$$|AB|=\sqrt{(5-1)^2+(3-2)^2}=\sqrt{16+1}=\sqrt{17}\approx4,123$$

Videolektion