Fordelingsfunktion og frekvensfunktion

Efter at have udført en statistisk undersøgelse, vælger man ofte at gruppere sit data.

Man kan plotte sine data i et histogram med lige bredde søjler. I dette tilfælde svarer søjlens højde til frekvensen. Imidlertid bestemmer man selv, hvor bredde ens intervaller skal være.

Hvis man gør sine intervaller smallere og smallere, vil histogrammet til sidst blive tilpasset en glat kurve.

Den glatte kurve, de tilpasses kaldes frekvensfunktionen eller tæthedsfunktionen. Dette skyldes, at den for hver observation (x-værdi) siger hvor høj en frekvens (y-værdi), denne observation har.

Fordelingsfunktion

På samme måde hvis vi indtegner de kumulerede frekvenser for data i en sumkurve. Jo smallere vi gør intervallerne, des mere glat bliver sumkurven. Den glatte kurve er graf for fordelingsfunktionen.

Sammenhæng mellem frekvensfunktion og fordelingsfunktion

I afsnittet om sumkurver så vi, at vi ud for hver x-værdi kunne aflæse hvor mange procent i undersøgelsen, der var mindre end eller lig med denne værdi.

På samme måde svarer fordelingsfunktionens værdi i et bestemt punkt til, hvor mange procent af målingerne, der er mindre end eller lig med denne observation.

Men dette svarer jo til den kumulerede frekvens for denne observation. Det svarer altså til at lægge frekvenserne sammen for alle de observationer, der er mindre end eller lig med vores faste punkt. Dette er jo summen af arealet af søjlerne i histogrammet, svarende til arealet under frekvensfunktionen til venstre for det faste punkt.

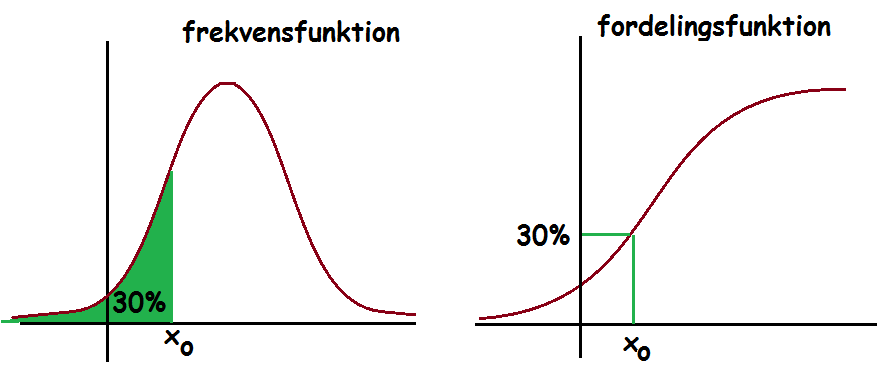
Med brug af integralregning får man altså denne sammenhæng mellem fordelings- og frekvensfunktion.

$$\text{Fordelingsfunktion}(x_0)=\int_{-\infty}^{x_0}\text{frekvensfunktion}(x)\:dx$$