Sinusrelationerne
Ofte kommer man ud for opgaver, hvor man i en trekant kender nogle sider og vinkler og bliver bedt om at finde nogle andre sider eller vinkler. Til at løse den slags opgaver er sinusrelationerne et stærkt værktøj.
Det, der gør sinusrelationerne til et stærkt redskab, er, at de gælder i vilkårlige trekanter. Det er altså ligegyldigt, om den trekant, vi arbejder med, er retvinklet, ligebenet, ligesidet eller ingen af delene. Vi kan bruge sinusrelationerne til dem alle sammen.
Hvis vi vil finde en side
Hvis vi kender to vinkler og den side, der står over for den ene, så kan vi bestemme den side, der står over for den anden vinkel ved hjælp af følgende formel.
$$\frac{a}{\sin(A)}=\frac{b}{\sin(B)}=\frac{c}{\sin(C)}$$
For eksempel kunne vi blive bedt om at finde siden c i følgende trekant
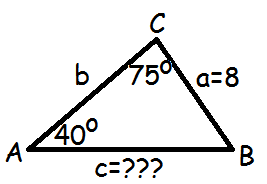
Vi kender vinklerne A og C samt den side, der står overfor vinkel A. Vi bruger sinusrelationerne. Vi tager kun de ting med, der er relevante for os, så i vores tilfælde udelader vi b'erne.
$$\frac{c}{\sin(C)}=\frac{a}{\sin(A)}$$
Vi starter med at isolere c ved at gange med sin(C) på begge sider.
$$c=\frac{a\cdot\sin(C)}{\sin(A)}$$
Nu sætter vi tal ind på pladserne
$$c=\frac{8\cdot\sin(75^\circ)}{\sin(40^\circ)}$$
$$c=\frac{8\cdot0,966}{0,643}\approx12,02$$
Hvis vi skal finde en vinkel
Hvis vi kender to sider og en vinkel, der står over for en af siderne, så kan vi finde den vinkel, der står over for den anden side. Vi bruger disse formler.
$$\frac{\sin(A)}{a}=\frac{\sin(B)}{b}=\frac{\sin(C)}{c}$$
Forskellen mellem disse og dem, vi nævnte ovenfor, er, at man har byttet rundt på alle tællere og nævnere. Det er altid smartest, at det man skal finde står i tælleren!
Lad os se på et eksempel. Vi bliver bedt om at finde vinkel B i følgende trekant.
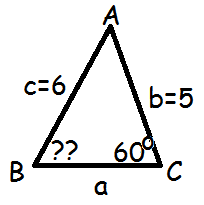
Vi kender siderne b og c samt den vinkel, der ligger over for c. Så kan vi finde b ved hjælp af sinusrelationerne. Vi skriver kun de dele op, vi har brug for, og undlader således a'erne.
$$\frac{\sin(B)}{b}=\frac{\sin(C)}{c}$$
Vi isolerer sin(B) ved at gange med lille b på begge sider
$$\sin(B)=\frac{b\cdot\sin(C)}{c}$$
Nu sætter vi tal ind
$$\sin(B)=\frac{5\cdot\sin(60^\circ)}{6}$$
$$\sin(B)=\frac{5\cdot0,866}{6}\approx0,722$$
Vi ved nu, hvad sin(B) er. For at finde B tager vi sin-1 til dette tal.
$$\sin(B)=0,722$$
$$B=\sin^{-1}(0,722)$$
$$B=46,19^\circ$$
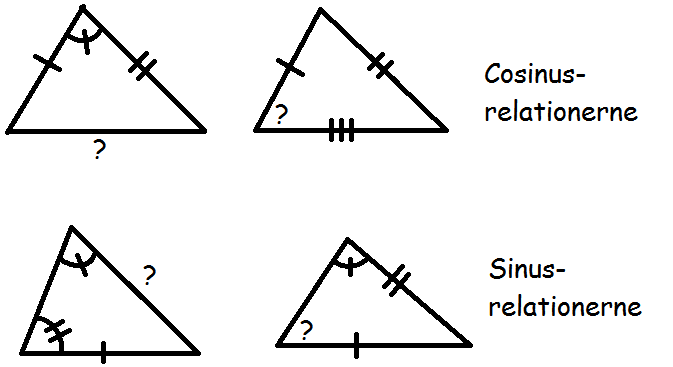
Skal jeg bruge cosinus- eller sinusrelationerne?
Her er en oversigt over, hvornår det er smartest at bruge hhv. cosinus- og sinusrelationerne. De vinkler og sider, der er markeret med streger, er de ting, vi kender på forhånd. Spørgsmålstegnene markerer de sider eller vinkler, vi er interesserede i at finde.