\(R^2\)
I forrige afsnit viste vi en måde at finde den funktion, der bedst passer på en række koordinatsæt. At vi har fundet den bedste funktion til at beskrive en mængde koordinatsæt betyder dog ikke, at der er en sammenhæng mellem de to variable. I eksemplet vi brugte før, ser det ud som om, der er en sammenhæng, men vi vil gerne have et mål for sammenhængen.
Det første skridt er, at finde det samlede areal, under antagelse af, at der ikke er en sammenhæng mellem de to variable. Her måler vi ikke afstanden til en funktion \( y = a \cdot x\), men derimod \(\bar{y}\). Her er \(\bar{y}\) lig den gennemsnitlige y-værdi for alle koordinatsættene. I vores eksempel er \(\bar{y} = \frac{2+7+15}{3} = 8\).
Ved at bruge \(\bar{y}\) til at finde det samlede areal hvis de er uafhængige, \(T_u\), får vi:
\((2 - 8)^2 + (7 - 8)^2 + (15 - 8)^2 = 86\)
Det er tydeligvis en meget dårligere funktion end den vi fandt tidligere. For at få et generelt udtryk for, hvor stor sammenhængen mellem variablerne er, skal vi nu finde det der hedder R^2-værdien. Den kan beskrives som følgende, der altid giver et tal mellem 0 og 1. Jo tættere på 1, jo bedre er sammenhængen.
\(R^2 = 1 - \frac{T}{T_u}\)
Inden for forskellige videnskaber har man forskellige krav for hvor god en sammenhæng skal være, før den er ’gyldig’. I naturvidenskab sigter man efter en \(R^2\) på mere end 0,95 – hvorimod man inden for samfundsvidenskaben ofte godtager sammenhænge fra 0,65 og op.
I vores eksempel er vores \(R^2\) lig:
\(R^2 = 1 - \frac{T}{T_u} = 1 - \frac{T(\frac{270}{132})}{86} = \frac{1851}{1892} \approx 0,98\)
Hvilket er udtryk for en meget stærk sammenhæng.
Et tilfælde med en dårlig sammenhæng er afbilledet herunder.
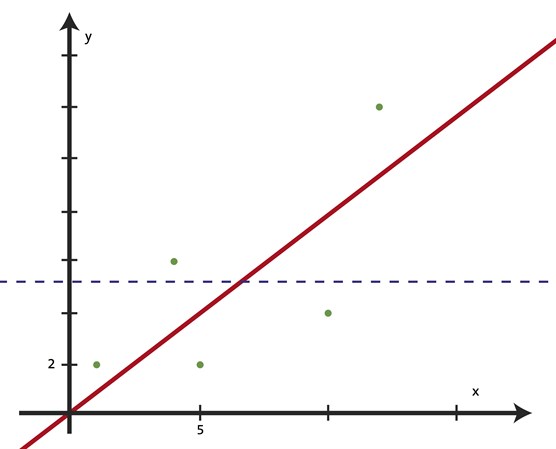
Den røde linje er den funktion, der bedst forklarer den proportionelle sammenhæng (fundet på den måde, der er beskrevet tidligere). Den har forskriften \(y = \frac{10}{13} \cdot x\), og den stiplede blå linje er den gennemsnitlige y-værdi. R2-værdien for dette eksempel er 0,49 - hvilket er meget lavt. Der er altså ikke tale om en proportionel sammenhæng. Dette udelukker dog ikke en anden type sammenhæng som f.eks. eksponentiel.
