Chi i anden-test

Nogle gange laver man et forsøg, hvor man på forhånd har en idé om, hvordan udfaldene bør være. Man kan derfor teste, om de observerede værdier stemmer overens med de forventede værdier. Til at gøre det, kan man bruge χ²-test (χ er det græske tegn chi (og altså ikke et x)).

Vi vil her gennemgå, hvordan et χ²-test fungerer vha. et eksempel.

Vi kaster 60 terninger og får resultaterne

Antal øjne	1	2	3	4	5	6
Antal terninger	5	12	11	16	7	9

Forventede værdier

Når man laver et χ2-test, er det første, man skal gøre, at beregne sine forventede værdier.

I vores tilfælde havde vi regnet med at terningerne ville fordele sig med 1/6 (dvs 10 terninger) ud for hvert antal øjne.

Vi tilføjer en række med forventede værdier

Antal øjne	1	2	3	4	5	6
Antal terninger	5	12	11	16	7	9
Forventet	(1/6\(\cdot\)60=) 10	10	10	10	10	10

Nu er det store spørgsmål: skyldes afvigelsen tilfældigheder, eller er der noget galt med vores terninger (eller den måde vi kastede dem på)?

Nulhypotese

Først opstiller man en nulhypotese, H₀.

Den vil typisk være, at forskellen mellem de forventede og observerede værdier skyldes tilfældigheder.

Hvis vi ender med at forkaste vores nulhypotese, kan vi altså sige, at der er en signifikant forskel mellem forventet og observeret.

Hvis vi ender med ikke at forkaste (dvs. acceptere) vores nulhypotese, kan vi sige, at der ikke er nogen signifikant forskel på forventede og observerede data.

Vores nulhypotese er:
H₀: Antallet af terninger, der viser et bestemt antal øjne er uafhængigt af, hvilket antal øjne, de viser.Eller med andre ord: der er lige stor sandsynlighed for at få hvert antal øjne.

Valg af signifikansniveau

Før man laver testet, skal man blive enig med sig selv om, hvad der skal til, før man forkaster hypotesen.

Udkommet at testet er en procentsats.
Den angiver, hvor stor sandsynligheden er for at få data, der passer lige så godt eller dårligere til nulhypotesen end de observerede data - under forudsætning af, at nulhypotesen er sand.

Typisk vil man vælge et signifikansniveau på 5%. Dvs. at hvis der (givet at nulhypotesen er sand) er mindre end 5% chance for at få de observerede data, så forkaster vi hypotesen.

Man kan også sige, at signifikansniveauet er risikoen for at forkaste en sand hypotese. Hvis vi gentog vores eksperiment mange gange, ville vi altså i 5% af tilfældene komme til at forkaste vores hypotese, selvom den var sand.

Det kan foranledige en til at vælge et lavere signifikansniveau. Men jo lavere man sætter sit signifikansniveau, des sværere bliver det at forkaste nulhypotesen, og derved øger man risikoen for at godtage en nulhypotese, selvom den faktisk er falsk.

Det er derfor en afvejning, hvor man sætter sit signifikansniveau, og det er normen at man bruger et signifikansniveau på 5%. Medicinske forsøg kræver dog tit et signifikansniveau på 1%.

Jo større forsøg man laver, des mindre bliver risikoen for både at afvise en sand hypotese og godkende en falsk hypotese. (Hvis vi f.eks. havde kastet 600 terninger i stedet for 60)

Frihedsgrader

Til et χ²-test er knyttet et antal frihedsgrader.
Hvis der er k observationer, er der k-1 frihedsgrader.
I vores tilfælde er der 6 observationer, og derved er der 5 frihedsgrader.

Det betyder egentlig, at hvis vi tilfældigt skal fordele 60 terninger i de 6 bokse, så kan vi selv vælge hvor mange terninger vi kommer i hver af de fem første bokse, men i den sidste har vi ingen valgfrihed, den skal nemlig indeholde forskellen mellem 60 (det totale antal) og det vi har brugt på de 5 første.

Udregne χ²-teststørrelsen

Nu er vi kommet til dér, hvor testet rigtigt starter. Nemlig beregningen af vores teststørrelse. Den beregnes ud fra følgende formel:

$$\chi^2=\sum_{i=1}^k\frac{(O_i-F_i)^2}{F_i}=\frac{(O_1-F_1)^2}{F_1}+\frac{(O_2-F_2)^2}{F_2}+...+\frac{(O_k-F_k)^2}{F_k}$$

hvor O står får observeret værdi, og F for forventet værdi.

Det er klart, at jo lavere χ²-teststørrelsen er, des tættere ligger de observerede værdier på de forventede.
Vi udregner χ²-teststørrelsen for vores terningforsøg.

$$\chi^2=\frac{(5-10)^2}{10}+\frac{(12-10)^2}{10}+\frac{(11-10)^2}{10}+\frac{(16-10)^2}{10}+\frac{(7-10)^2}{10}+$$

$$\frac{(9-10)^2}{10}=7,6$$

Vores teststørrelse er altså 7,6.

Konklusion på test

Når vi har fundet vores χ²-teststørrelse skal vi have omsat den til en konklusion på testet.

Der er to måder at gøre det på.

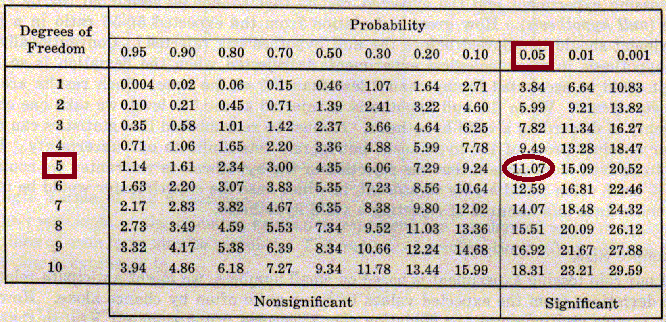
Den første (der er mest gammeldags og mest intuitiv) er at benytte et  χ²-skema. Man aflæser sin kritiske værdi ud for antallet af frihedsgrader og signifikansniveau.

I vores terningforsøg var der 5 frihedsgrader og vi havde valgt et signifikansniveau på 5% (0,05).

Vi kan dermed aflæse vores kritiske værdi til 11,07.

Hvis vores teststørrelse er større end den kritiske værdi, forkaster vi nulhypotesen, og hvis den er lavere, accepterer vi den.

Vores χ²-teststørrelse var 7,6, der er lavere end 11,07, og derfor accepterer vi nulhypotesen.

Den anden måde at konkludere på i χ²-testet er ved at finde p-værdien: sandsynligheden for at de observerede data optræder givet at nulhypotesen er sand.

Den kan bl.a. findes i Excel ved at skrive =CHIFORDELING(teststørrelse;frihedsgrader)

I vores tilfælde ville det give

$$\\''=\text{CHIFORDELING}(7,6\:;\:5)''=0,18=18\%\\$$

Det vil sige, at hvis nulhypotesen er sand, er der 18 % chance for at vores data (eller noget der er værre) optræder. Da de 18 % er højere end vores signifikansniveau på 5%, accepterer vi hypotesen.

Opsamling

-  Find forventede værdier
-  Opstil H₀
-  Vælg signifikansniveau og find antal frihedsgrader
-  Udregn teststørrelse

Og herefter:
- Aflæs kritisk værdi i χ²-skema. Hvis teststørrelsen er større end den kritiske værdi, afviser vi H_0.
- Eller find p-værdi. Hvis p-værdien er mindre end signifikansniveauet, afviser vi H₀.