Afstandsformlen
Afstandsformlen er en formel til at finde afstanden mellem to punkter, hvis vi blot kender deres koordinatsæt.
Hvis punktet A har koordinaterne (x1, y1) og punktet B har koordinaterne (x2, y2), så er afstanden mellem punkterne:
$$|AB|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$
De lodrette linjer betyder "afstanden mellem A og B" eller "længden af linjestykket mellem A og B".
Hvis f.eks. A(1, 2) og B(3, 5), så er
$$|AB|=\sqrt{(3-1)^2+(5-2)^2}=\sqrt{2^2+3^2}=\sqrt{13}\approx3,61$$
Hvorfor ser formlen ud, som den gør?
Grunden til, at formlen ser ud, som den gør, skyldes Pythagoras. Hvis vi ud fra vores ene punkt tegner en vandret stiplet linje, og ud fra det andet tegner en lodret stiplet linje, så vil de to linjer mødes, og der vil dannes en retvinklet trekant.
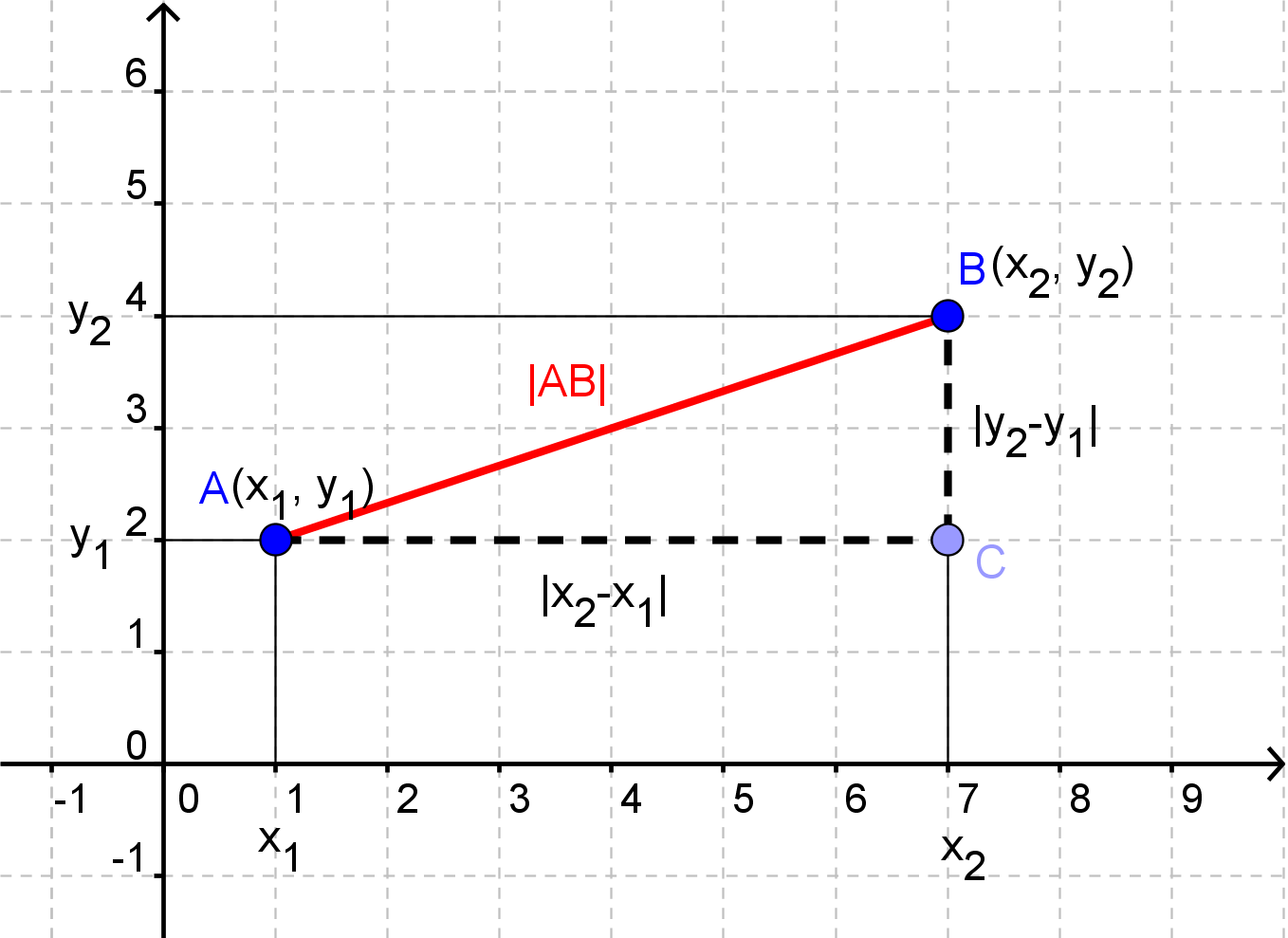
Det er let at finde længden af kateterne. Den enes længde er forskellen i x-koordinaterne, og den andens er forskellen i y-koordinaterne.
Nu følger formlen ved at bruge Pythagoras' læresætning
$$\text{hyp}^2=1.\text{kat}^2+2.\text{kat}^2$$
$$|AB|^2=|x_2-x_1|^2+|y_2-y_1|^2$$
$$|AB|^2=(x_2-x_1)^2+(y_2-y_1)^2$$
Så skal vi til sidst tage kvadratroden på begge sider
$$|AB|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$
OBS: Formlen gælder også, selvom linjestykket mellem punkterne er parallelt med x- eller y-aksen.
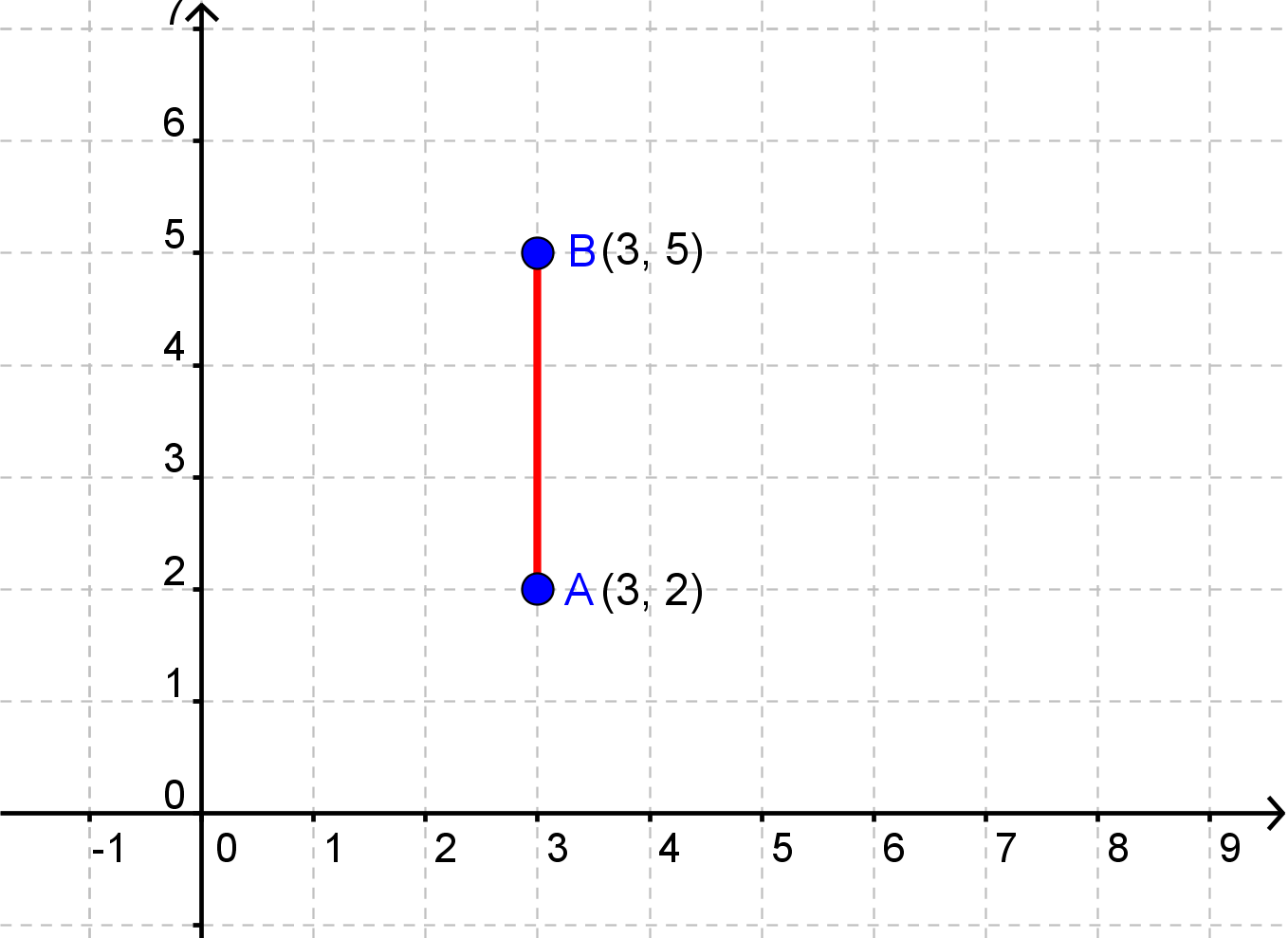
$$|AB|=\sqrt{(3-3)^2+(5-2)^2}=\sqrt{0+3^2}=3$$
