Arealformlen
Indenfor trigonometrien findes der en smart måde at regne arealet af en trekant ud, hvis man blot kender to sider og den mellemliggende vinkel. Man betegner tit arealet af en trekant med T (hvis man brugte A ville man nemlig forveksle det med vinkel A).
$$T=\frac{1}{2}ab\sin(C)$$
For lettere at kunne huske denne formel, kaldes den ofte for "en halv appelsin"-formlen - prøv selv at udtale højresiden og find ud af hvorfor.
Formlen gælder i vilkårlige trekanter, og man kan derfor også udtrykke den ved de andre sider og vinkler.
$$T=\frac{1}{2}ab\sin(C)=\frac{1}{2}bc\sin(A)=\frac{1}{2}ac\sin(B)$$
Lad os tage et eksempel.
Vi ønsker at finde arealet af denne trekant
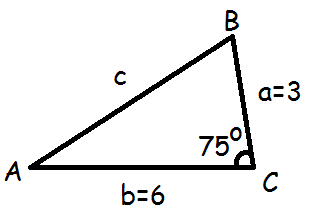
Vi kender to sider (a og b) samt den mellemliggende vinkel (C). Derfor kan vi beregne arealet ved hjælp af "en halv appelsin"-formlen
$$T=\frac{1}{2}ab\sin(C)$$
$$T=\frac{1}{2}\cdot3\cdot6\cdot\sin(75^\circ)$$
$$T=9\cdot0,966$$
$$T\approx8,69\:\text{arealenheder}$$
Hvorfor ser formlen sådan ud?
Det er let at bevise ½ appelsin-formlen. Vi husker på, at arealet af en trekant er en halv højde gange grundlinje.
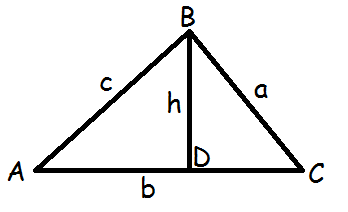
På ovenstående tegning er b grundlinje til højden h.
$$T=\frac{1}{2}bh$$
Trekanten BDC er retvinklet, og derfor kan vi bruge regnereglerne for sinus i retvinklede trekanter.
$$\sin(v)=\frac{\text{modstående katete}}{\text{hypotenuse}}$$
$$\sin(C)=\frac{h}{a}\quad\Leftrightarrow\quad h=a\cdot\sin(C)$$
Dette sætter vi ind på h's plads
$$T=\frac{1}{2}bh=\frac{1}{2}b\cdot a\cdot\sin(C)=\frac{1}{2}ab\sin(C)$$
og så er formlen bevist. (Hvis vi ville have vist den med nogle af de andre sider, kunne vi have taget udgangspunkt i en anden højde).
