Tretrinsreglen
Tretrinsreglen er en metode til, hvordan man differentierer funktioner. Den er en kombination af afsnittene funktionstilvækst og differenskvotient og differentialkvotient herover, så det anbefales at du læser dem først.
Tretrinsreglen består - som navnet antyder - af tre trin.
Trin 1: Find funktionstilvæksten
$$\Delta y=f(x_0+h)-f(x_0)$$
Trin 2: Find differenskvotienten
$$a_s=\frac{\Delta y}{h}=\frac{f(x_0+h)-f(x_0)}{h}$$
Trin 3: Find differentialkvotienten
$$a_t=f'(x_0)=\lim_{h\to0}(a_s)=\lim_{h\to0}\big(\frac{f(x_0+h)-f(x_0)}{h}\big)$$
I stedet for at indsætte et bestemt tal på x0's plads, så plejer man at tage udgangspunkt i et tilfældigt x0. Resultatet bliver således en funktion, der kaldes den afledede funktion. Ved at indsætte et punkt i den afledede funktion, finder man hældningen i det punkt.
Eksempel
Vores funktion er f(x)= 3x2
Trin 1:
Vi starter med at finde f(x0+h) ved at sætte x0+h ind på x's plads i funktionsudtrykket.
$$f(x_0+h)=3(x_0+h)^2=3(x_0^2+h^2+2x_0h)=3x_0^2+3h^2+6x_0h$$
Vi brugte undervejs en kvadratsætning
Nu finder vi f(x0)
$$f(x_0)=3x_0^2$$
Vi finder funktionstilvæksten ved at trække dem fra hinanden
$$\Delta y=f(x_0+h)-f(x_0)=(3x_0^2+3h^2+6x_0h)-(3x_0^2)=3h^2+6x_0h$$
Trin 2:
Nu finder vi differenskvotienten (dvs. sekanthældningen)
$$a_s=\frac{\Delta y}{h}=\frac{3h^2+6x_0h}{h}=\frac{h(3h+6x_0)}{h}=3h+6x_0$$
Undervejs satte vi et h uden for parentes i tælleren for at kunne reducere brøken med h (lade h i tælleren gå ud med h i nævneren)
Trin 3:
Til sidst skal vi finde differentialkvotienten.
Vi skal altså undersøge, hvad der sker med differenskvotienten, når h bliver uendelig lille. Når h bliver uendelig lille, så bliver 3h også uendelig lille. Derfor kan vi se bort fra 3h. Derimod bliver 6x0 overhovedet ikke påvirket af, hvor stor h er.
$$a_t=\lim_{h\to0}(a_s)=\lim_{h\to0}(3h+6x_0)=6x_0$$
Differentialkvotienten er dermed
$$f'(x_0)=6x_0$$
Det betyder, at hvis vi vil finde hældningen i et bestemt punkt, så indsætter vi det bare på x0's plads, og så finder vi hældningen. F.eks. er hældningen, når x0=0,5
$$f'(0,5)=6\cdot0,5=3$$
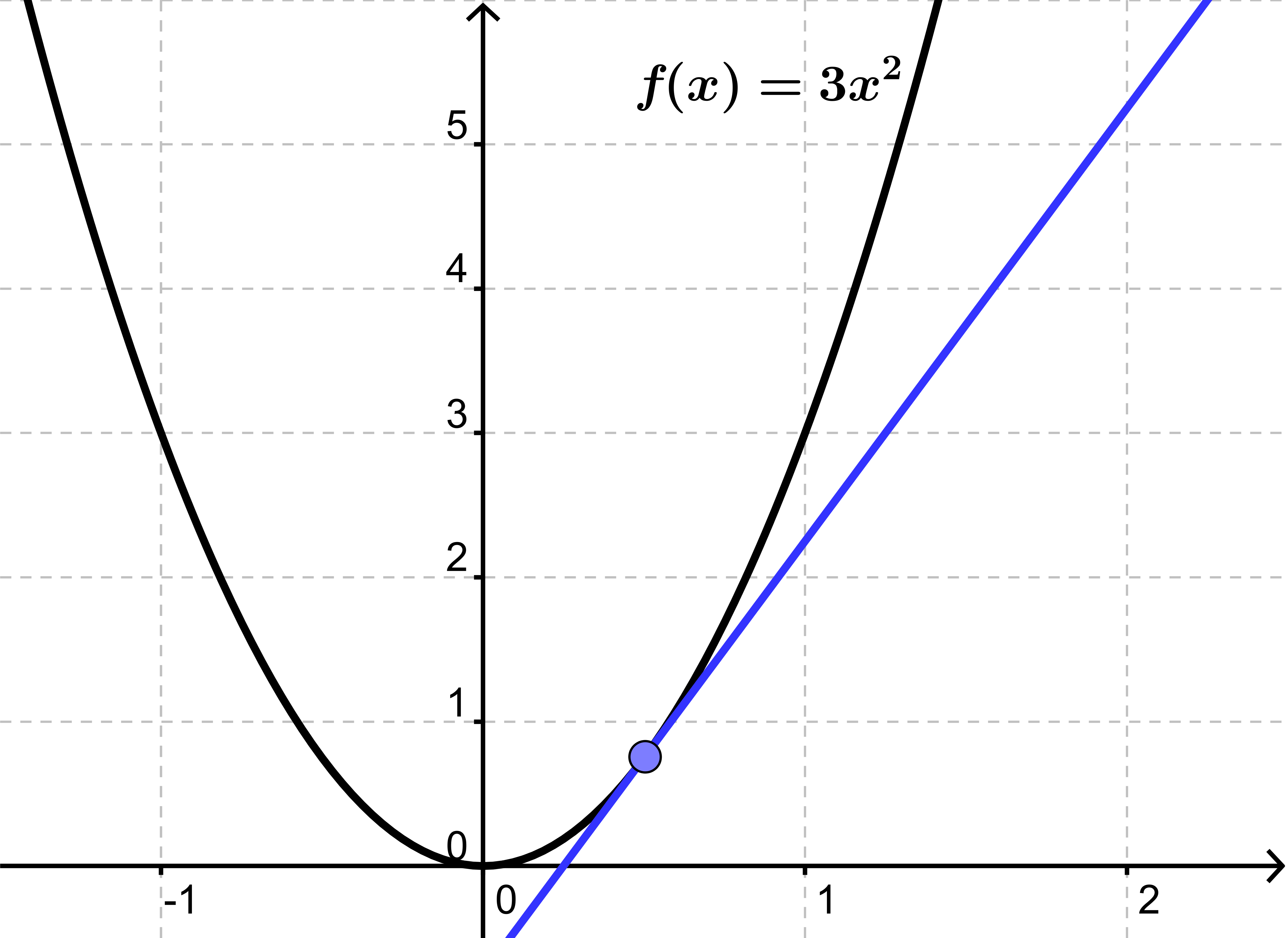
Dette kan vi også aflæse på nedenstående tegning, hvor f er tegnet ind samt tangenten i punktet
x0=0,5