Cirkler og linjers skæringer
Cirkler
En cirkel er en punktmængde, hvorom der gælder, at alle punkter på cirklen har samme afstand til et punkt kaldet cirklens centrum. Denne afstand kaldes radius. Skrevet med mængdesymboler ser det således ud
$$\mathcal{C}(C,r)=\left\{P=(x,y)\:\left|\:|PC|=r\right.\right\}$$
Hvis man skulle udtale det, ville det lyde "Cirklen med centrum \(C\) og radius \(r\) er mængden af punkter \(P\), hvorom der gælder, at afstanden mellem \(P\) og \(C\) er \(r\)".
Bemærk, at centrum ikke er en del af cirklen. Cirklen er udelukkende periferien.
Hvis centrumskoordinaterne er \(C(a, b)\) kan vi omregne betingelsen for at \(P(x, y)\) ligger på cirklen.
$$\begin{align}
r & = |PC| \\
r & = |\overrightarrow{PC}| \\
r & = |\overrightarrow{CP}| \\
r & = \left|\begin{pmatrix}x-a\\y-b\end{pmatrix}\right|\\
r & = \sqrt{(x-a)^2+(y-b)^2} \\
r^2 & = (x-a)^2+(y-b)^2.
\end{align}$$
En cirkel er altså alle punkter \((x, y)\) der opfylder ligningen
$$(x-a)^2+(y-b)^2=r^2$$
Skæring mellem cirkel og linje givet ved ligning
Hvis vi har oplyst cirklens centrum og radius samt linjens ligning, kan vi finde ud af, om der er nogen skæringer mellem cirklen og ligningen. Vi bruger simpelthen dist-formlen til at finde den korteste afstand mellem linjen og cirklens centrum. Hvis afstanden er større end radius, er der ingen skæringer, hvis afstanden er lig med radius, er der et røringspunkt (linjen er i så fald tangent til cirklen), hvis afstanden er mindre end radius, er der to skæringspunkter.
Hvis vi blev spurgt, hvor mange skæringer der var mellem
$$\mathcal{C}:(x+2)^2+(y-3)^2=16\text{ og } l:4x-5y+6=0$$
så ville vi starte med at aflæse radius til \(r=4\) og centrumkoordinaterne til \(C=(-2, 3)\). Man skal holde tungen lige i munden med fortegnene til koordinaterne! Nu sætter vi ind i dist-formlen
$$\text{dist}(C,l)=\frac{|4\cdot(-2)-5\cdot3+6|}{\sqrt{4^2+5^2}}=\frac{|-17|}{\sqrt{16+25}}=\frac{17} {\sqrt{41}}\approx2,65<4$$
Da afstanden er mindre end radius, er der to skæringer mellem cirklen og linjen.
Skæringer mellem cirkel og linje givet ved parameterfremstilling
Hvis en linje er givet ved parameterfremstilling, kan vi ikke bruge dist-formlen til at bestemme antallet af skæringspunkter. I stedet kan vi indsætte parameterfremstillingen i cirklens ligning og dermed finde ud af for hvilke \(t\) (hvis nogen overhovedet) der er skæringer.
Det er lettest at gennemgå ved hjælp af et eksempel.
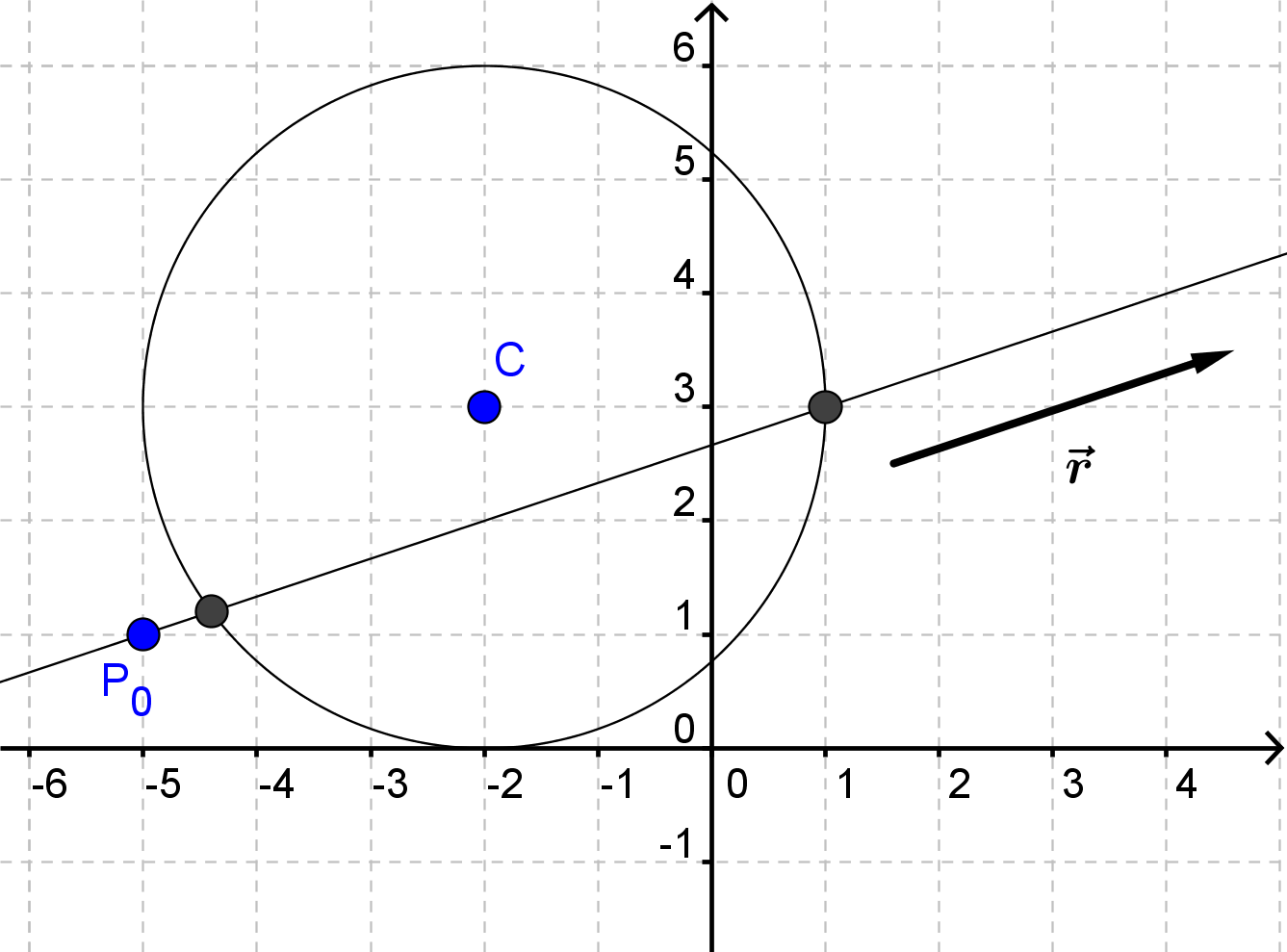
Vores cirkel er givet ved
$$\mathcal{C}:(x+2)^2+(y-3)^2=9$$
og vores linje er givet ved
$$l:\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}-5\\1\end{pmatrix}+t\cdot\begin{pmatrix}3\\1\end{pmatrix}$$
Vi starter med at skrive parameterfremstillingen om til koordinatfunktioner
$$x(t)=-5+3t\\y(t)=1+t$$
Disse sætter vi så ind på hhv. \(x\)'s og \(y\)'s plads i cirklens ligning
$$\begin{align}
(\underbrace{-5+3t}_x+2)^2+(\underbrace{1+t}_y-3)^2 & =9 \\
(3t-3)^2+(t-2)^2 & = 9 \\
(9t^2+9-18t)+(t^2+4-4t) & = 9 \\
10t^2-22t+13 & = 9 \\
10t^2-22t+4 & = 0.
\end{align}$$
Nu står vi med en andensgradsligning, hvor \(t\) er den ubekendte.
Vi starter med at finde diskriminanten. Hvis den er positiv er der to skæringer, hvis den er 0 er der et røringspunkt og hvis den er negativ skærer cirklen og linjen ikke hinanden.
$$d=(-22)^2-4\cdot10\cdot4=324$$
Der er altså to skæringspunkter.
Nu kan vi finde ud af for hvilke \(t\)-værdier skæringerne finder sted.
$$t=\frac{22\pm\sqrt{324}}{2\cdot10}=\frac{22\pm18}{20}=\begin{cases}
\frac{40}{20}=2 \\
\frac{4}{20}=0,\!2
\end{cases}
$$
Nu indsætter vi disse \(t\)-værdier i linjens parameterfremstilling for at finde skæringspunkternes koordinater.
$$t=2:\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}-5\\1\end{pmatrix}+2\cdot\begin{pmatrix}3\\1\end{pmatrix}=\begin{pmatrix}-5+2\cdot3\\1+2\cdot1\end{pmatrix}=\begin{pmatrix}1\\3\end{pmatrix}\\t=0,\!2:\begin{pmatrix}x\\y\end{pmatrix}=\begin{pmatrix}-5\\1\end{pmatrix}+0,\!2\cdot\begin{pmatrix}3\\1\end{pmatrix}=\begin{pmatrix}-5+0,\!2\cdot3\\1+0,\!2\cdot1\end{pmatrix}=\begin{pmatrix}-4,\!4\\1,\!2\end{pmatrix}$$
Cirkel og ligning skærer altså hinanden i \((1, 3)\) og \((-4,\!4, 1,\!2)\).