Definitions- og værdimængde
En funktion beskriver sammenhænge mellem variable. Vi kalder tit de variable for x og y. Man kan se funktioner som maskiner. Den uafhængige variabel, x, kommes ind i funktionen/makineriet, og så kommer den afhængige variabel, y, ud på den anden side. For hvert x må der kun være et y. Men der må godt være flere x'er der rammer det samme y. For mere om funktioner, klik her.
Definitionsmængde
Definitionsmængden er alle de tal, vi må komme ind i funktionen. Tit er det alle de reelle tal, men nogle gange er der visse tal, hvor det ikke giver mening at komme dem ind i funktionen. Vi betegner definitionsmængden Dm, og hvis vi vil skrive, at det er definitionsmængden for en funktion ved navn f, så skriver vi Dm(f).
Hvis vi f.eks. har funktionen
$$f(x)=\frac{1}{x}$$
så må vi ikke sætte x=0, fordi man aldrig må dividere med 0. Vores definitionsmængde er derfor
$$Dm(f)=]-\infty,0[\cup]0,\infty[$$
Tegnet mellem intervallerne betyder "foreningsmængde", dvs. at det er begge intervaller, der er definitionsmængden. Man kunne også skrive
$$Dm(f)=\mathbb{R}\backslash\{0\}$$
her betyder backslashen "bortset fra". Det vil sige, at definitionsmængden er alle de reelle tal bortset fra mængden, der består af tallet 0.
Et andet eksempel kunne være funktionen
$$g(x)=\frac{3}{x+1}+\frac{4\cdot x}{x-3}$$
Den første brøk får 0 i nævneren, når x=-1. Derfor er -1 ikke med i definitionsmængden.
Den anden brøk får 0 i nævneren, når x=3. Derfor er 3 heller ikke med i definitionsmængden.
Definitionsmængden kan altså skrives på følgende måder.
$$Dm(g)=\mathbb{R}\backslash\{-1,3\}$$
$$Dm(g)=]-\infty,-1[\cup]-1,3[\cup]3,\infty[$$
Det øverste læses som "de reelle tal bortset fra mængden bestående af tallene -1 og 3".
Lineære og eksponentielle funktioner har ikke nogen forbudte værdier. Deres definitionsmængde er derfor alle de reelle tal.
Værdimængde
Mens definitionsmængden er alle de tal, man må komme ind i funktionen (alle de mulige x-værdier), så er værdimængden alle de mulige funktionsværdier (y-værdier). Værdimængden betegnes Vm, og hvis vi vil skrive værdimængden for funktionen f, så skriver vi Vm(f).
Tit kan det være en fordel at se på grafen for at finde værdimængden.
En eksponentialfunktion har kun positive y-værdier.
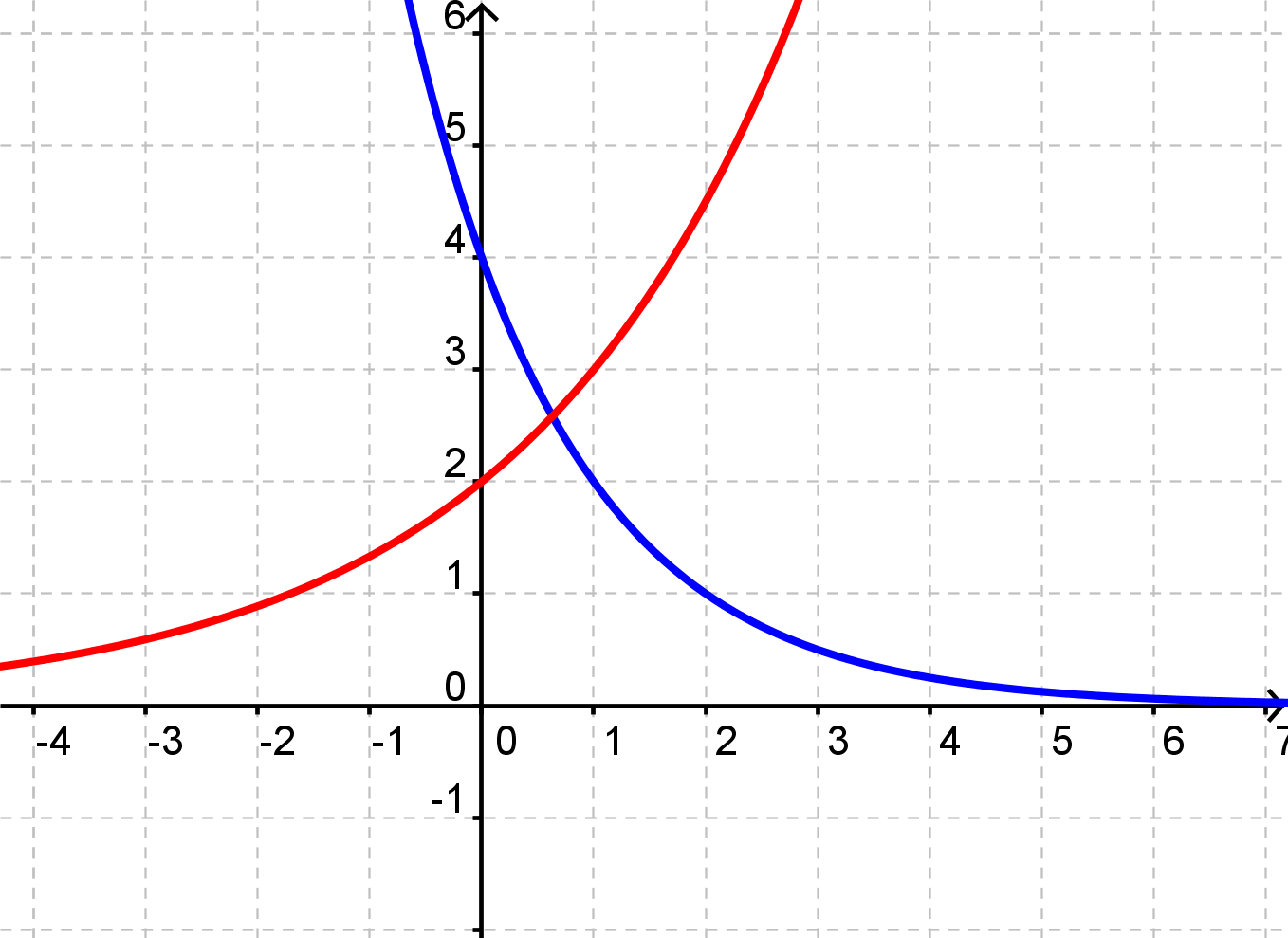
I koordinatsystemet er indtegnet en voksende og en aftagende eksponentialfunktion. De har begge positive y-værdier. Lige meget hvor stor en y-værdi man kunne tænke sig, kan man finde en x-værdi der passer til. Begge grafer smyger sig op af x-aksen (den røde ude mod venstre, den blå ude mod højre). De nærmer sig altså y-værdien 0, men de når aldrig helt derned. Derfor er 0 ikke med i værdimængden. Værdimængden for eksponentialfunktionen er derfor
$$Vm(f)=]0,\infty[$$
$$Vm(f)=\mathbb{R}_+$$
Det nederste skal læses som de positive reelle tal.
Et andet eksempel kunne være funktionen
$$f(x)=\frac{1}{x-1}$$
hvis graf er tegnet her
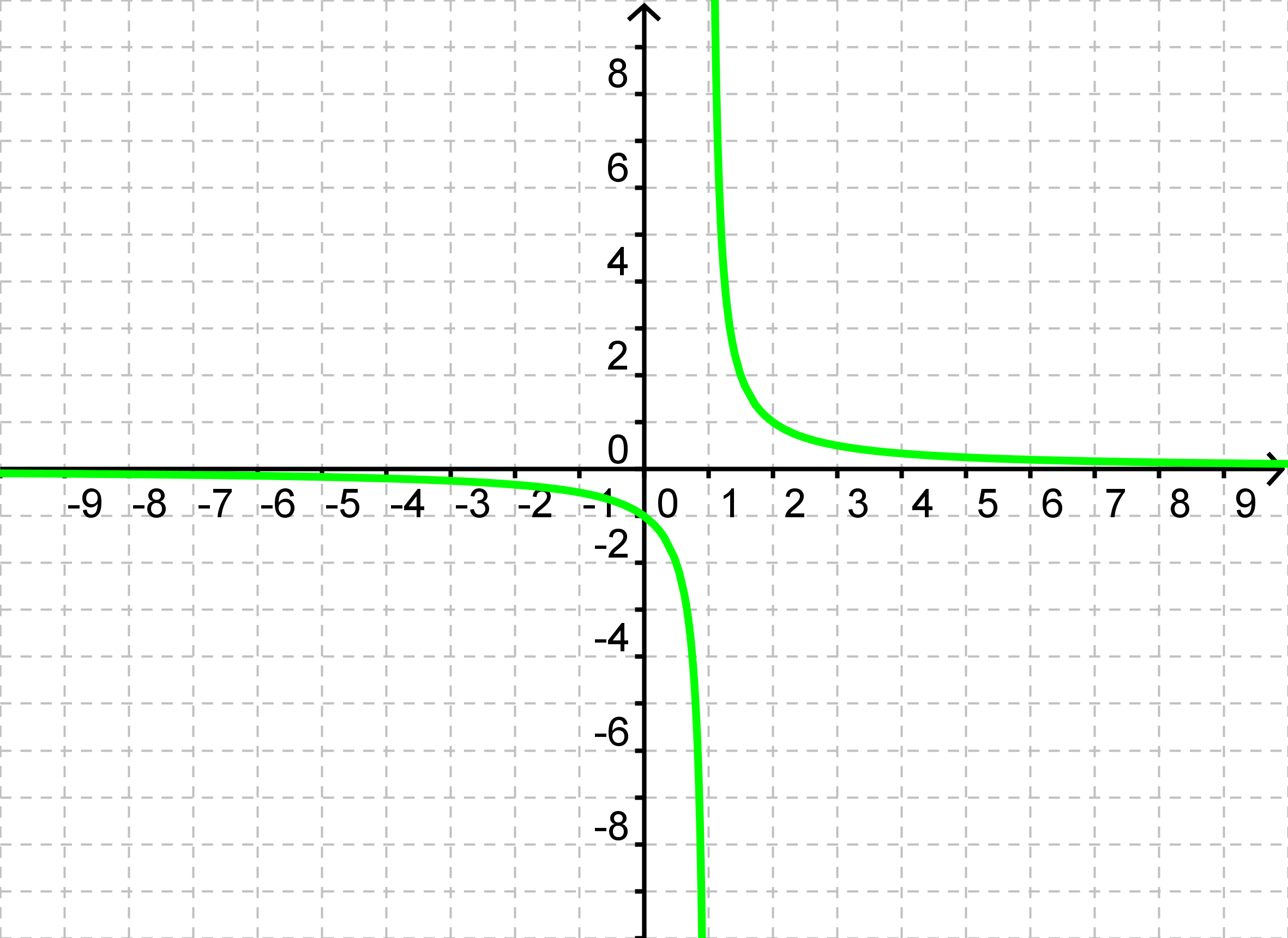
Ude til venstre smyger den sig op ad x-aksen, og funktionsværdierne er derfor tæt på 0, men dog en smule negative. Når vi bevæger os mod højre, falder funktionsværdierne, og når vi nærmer os x=1, bliver y-værdierne uendeligt små. Lige på den anden side af x=1 er funktionsværdierne pludselig uendeligt store, hvorfra de igen falder og nærmer sig 0. Til venstre for x=1 gennemløber vi altså alle de negative y-værdier, og til højre gennemløber vi alle de positive y-værdier. Værdimængden er altså alle de positive og negative reelle tal. Det vil sige alle de reelle tal bortset fra 0.
$$Vm(f)=]-\infty,0[\cup]0,\infty[$$
$$Vm(f)=\mathbb{R}\backslash\{0\}$$
Man kan også forestille sig en funktion hvis graf ser sådan her ud
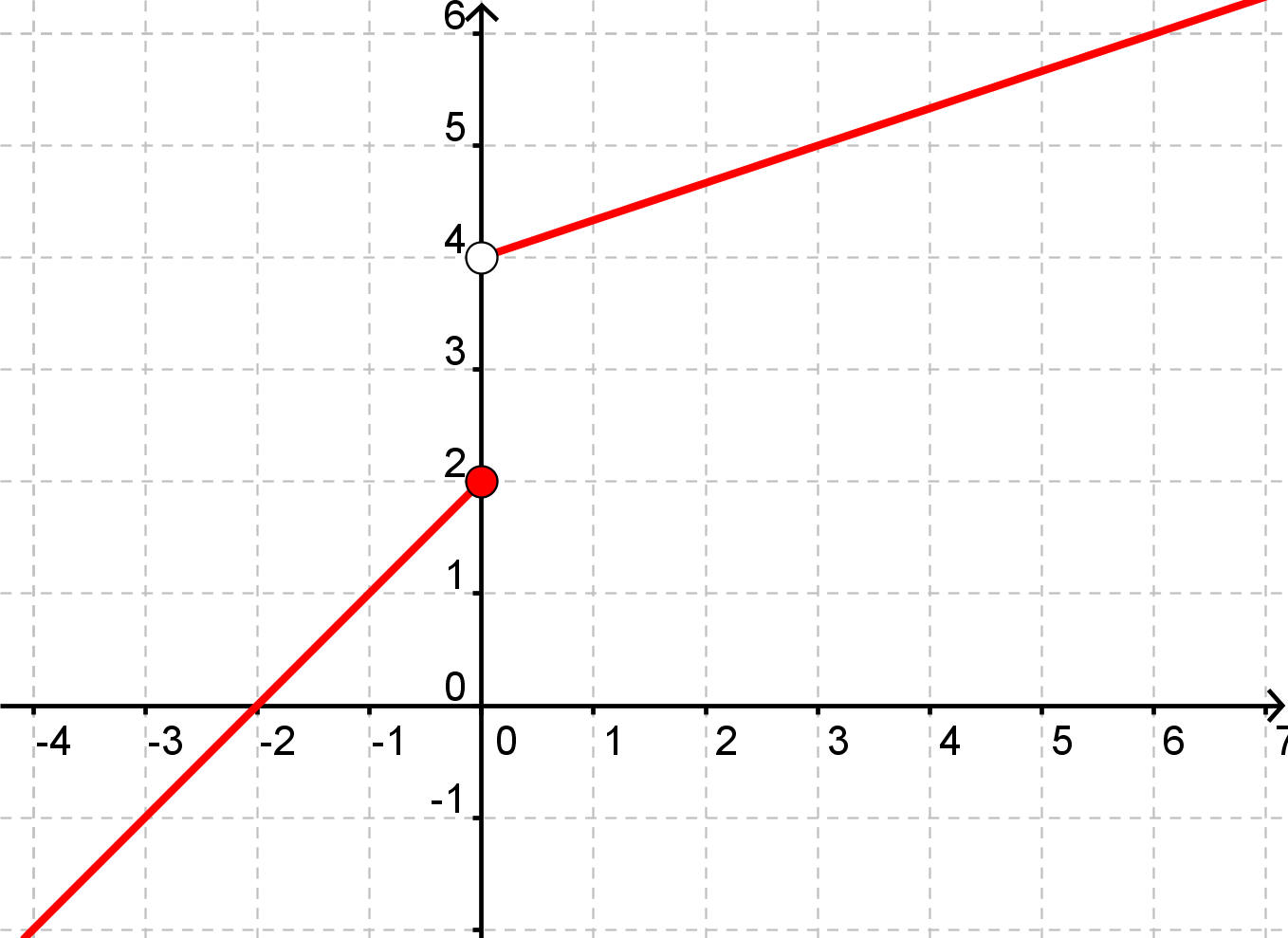
Definitionsmængden er alle de reelle tal, fordi funktionen er defineret for alle x-værdier. Men der er et interval på y-aksen som ikke er med i værdimængden. Man skal holde tungen lige i munden med om det er åbne eller lukkede intervaller, man har med at gøre. Tallet 2 er med i værdimængden, mens 4 ikke er.
$$Vm(f)=]-\infty,2]\cup]4,\infty[$$
$$Vm(f)=\mathbb{R}\backslash]2,4]$$
