Cosinus, Sinus og Tangens i retvinklede trekanter
I de forrige afsnit så vi, hvordan man definerer cosinus, sinus og tangens. I dette afsnit skal vi se, hvordan man kan bruge dem til at beregne sider og vinkler i retvinklede trekanter.
Det viser sig nemlig, at hvis v er en vinkel i en retvinklet trekant, så vil
$$\cos(v)=\frac{\text{hosliggende katete}}{\text{hypotenusen}}$$
$$\sin(v)=\frac{\text{modstående katete}}{\text{hypotenusen}}$$
$$\tan(v)=\frac{\text{modstående katete}}{\text{hosliggende katete}}$$
Grunden til, at det forholder sig sådan, er, at hvis vi har en retvinklet trekant ΔABC (som den blå nedenfor), kan vi tegne den ind i et koordinatsystem sammen med en enhedscirkel, således at vinkel A er i origo.
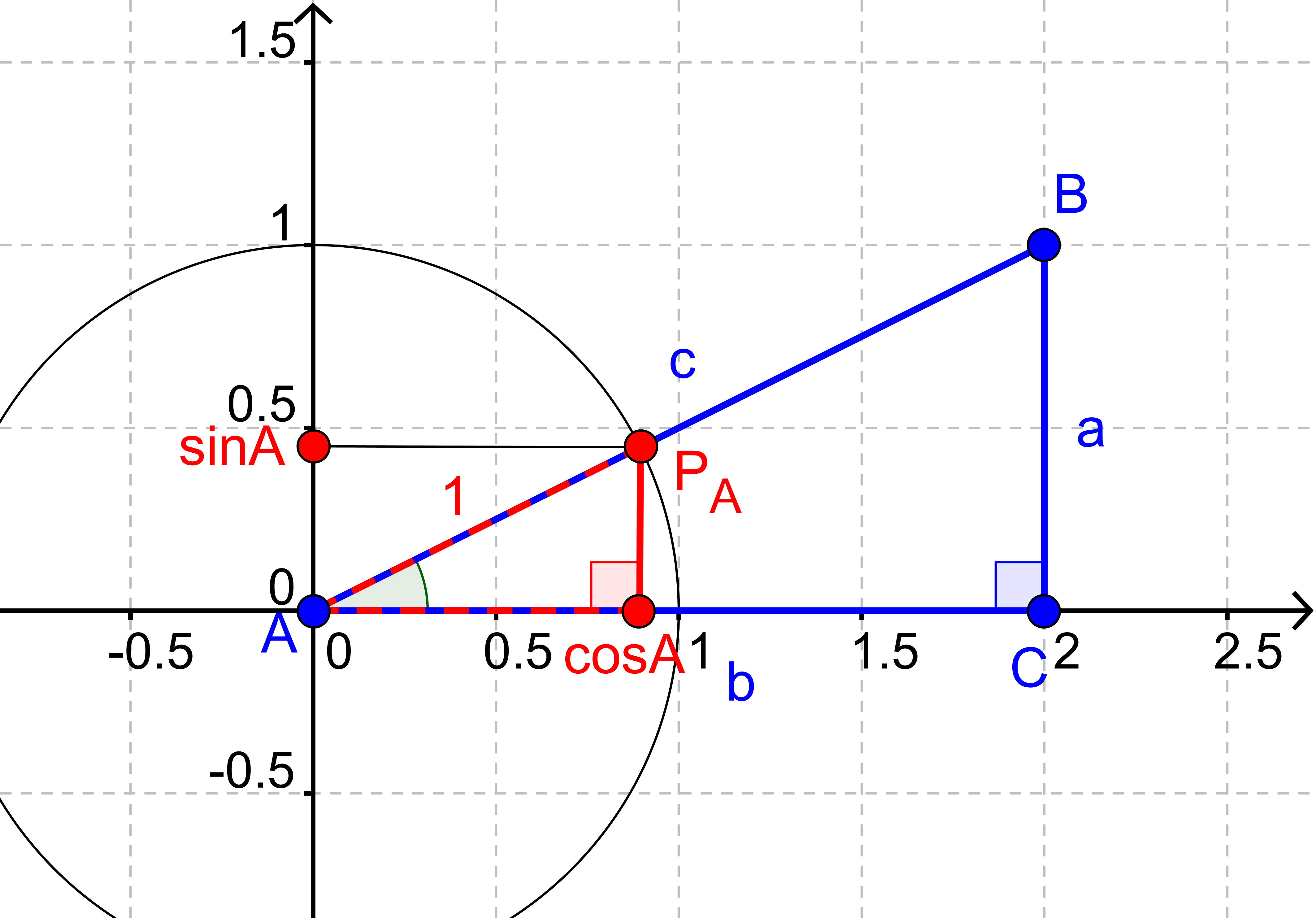
Den røde trekant på tegningen har sidelængderne cos(A), sin(A) og 1, (fordi linjestykket fra A til PA er en radius på enhedscirklen og derfor har længde 1)
Nu kan vi se, at vores oprindelige trekant (den blå) er ensvinklet med den røde (fordi de begge indeholder vinkel A og begge har en ret vinkel, så deres tredje vinkel også er nødt til at være ens).
Vi kan se, at
cos(A) er ensliggende med b,
sin(A) er ensliggende med a,
og 1 er ensliggende med c.
Nu bruger vi egenskaben ved ensvinklede trekanter, at forholdet mellem to sider i den ene trekant er lig med forholdet mellem de ensliggende sider i den anden trekant.
$$\frac{\cos(A)}{1}=\frac{b}{c}\Leftrightarrow\cos(A)=\frac{b}{c}$$
$$\frac{\sin(A)}{1}=\frac{a}{c}\Leftrightarrow\sin(A)=\frac{a}{c}$$
Vi kan også finde tangens til A:
$$\tan(A)=\frac{\sin(A)}{\cos(A)}=\frac{a:c}{b:c}=\frac{a}{b}$$
Altså de samme formler, som vi skrev øverst (da a er modstående katete, b er hosliggende katete og c er hypotenuse i den retvinklede trekant).
Lad os tage nogle eksempler.
Vi ønsker at finde v i følgende trekant.
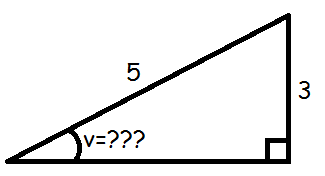
Vi ser at vi kender den modstående katete (modstående i forhold til vinkel v) og hypotenusen.
Derfor skal vi have fat i sinus.
$$\sin(v)=\frac{\text{modstående katete}}{\text{hypotenuse}}$$
$$\sin(v)=\frac{3}{5}=0,6$$
Nu tager vi sin-1 på begge sider for at finde frem til vinklen.
$$v=\sin^{-1}(0,6)$$
$$v=36,87^\circ$$
Et andet eksempel:
Vi ønsker at bestemme hypotenusen i følgende trekant.
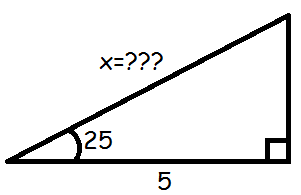
Vi kender den hosliggende katete (hosliggende i forhold til vinklen), og ønsker at bestemme hypotenusen. Altså er det cosinus, vi skal have fat i.
$$\cos(v)=\frac{\text{hosliggende katete}}{\text{hypotenuse}}$$
$$\cos(25^\circ)=\frac{5}{x}$$
$$x\cdot\cos(25^\circ)=5$$
$$x=\frac{5}{\cos(25^\circ)}$$
$$x\approx5,52$$
