Ligebenede og ligesidede trekanter
Hvis alle tre sider i en trekant er lige lange, kalder vi den ligesidet.
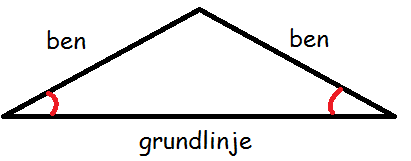
Hvis det kun er to af siderne, der er lige lange, så kalder vi den ligebenet. De to lige lange sider kalder vi for "benene", mens den tredje side kaldes for grundlinjen.
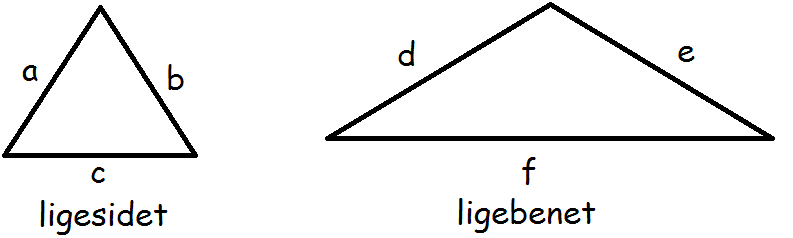
I den første trekant er alle tre sider lige lange, a=b=c
I den anden trekant er siderne d og e lige lange, d=e, mens vi ikke ved noget om hvor lang grundlinjen f er i forhold til dem.
Ligesidede trekanter
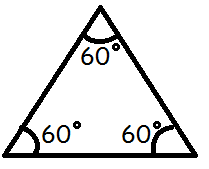
I ligesidede trekanter vil alle tre vinkler også være lige store. Og når vi husker at vinkelsummen i en trekant er 180º, så må hver vinkel i en ligesidet trekant være:
$$\frac{180^\circ}{3}=60^\circ$$
Ligebenede trekanter
I ligebenede trekanter vil de to vinkler, der ligger mellem benene og grundlinjen være ens.
Hvis vi f.eks. får at vide, at ΔABC er ligebenet, samt at vinklen overfor grundlinjen er 110º, og vi bliver bedt om at finde de to øvrige vinkler, kan vi gøre på følgende måde.
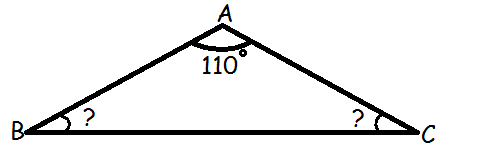
Vi ved, at vinkelsummen i en trekant er 180º. Derfor må
$$\angle B + \angle C+110^\circ=180^\circ$$
$$\angle B +\angle C=180^\circ-110^\circ$$
$$\angle B +\angle C=70^\circ$$
Altså ved vi nu, at de to vinkler tilsammen er 70º. Men fordi trekanten er ligebenet, ved vi, at de to vinkler ved grundlinjen er ens, og derfor må
$$\angle B=\angle C=\frac{70^\circ}{2}=35^\circ$$
således, at de hver er 35 grader.
