Find a og b (lineær)

Vi vil her gennemgå, hvordan man finder konstanterne a og b (hældningskoefficienten og skæringen med y-aksen), når man kender to punkter på grafen.

Lad os starte med at kalde de to punkter på grafen for hhv.

$$\left ( x_1, \,y_1 \right )\, \text{og}\, \left (x_2,\,y_2 \right )$$

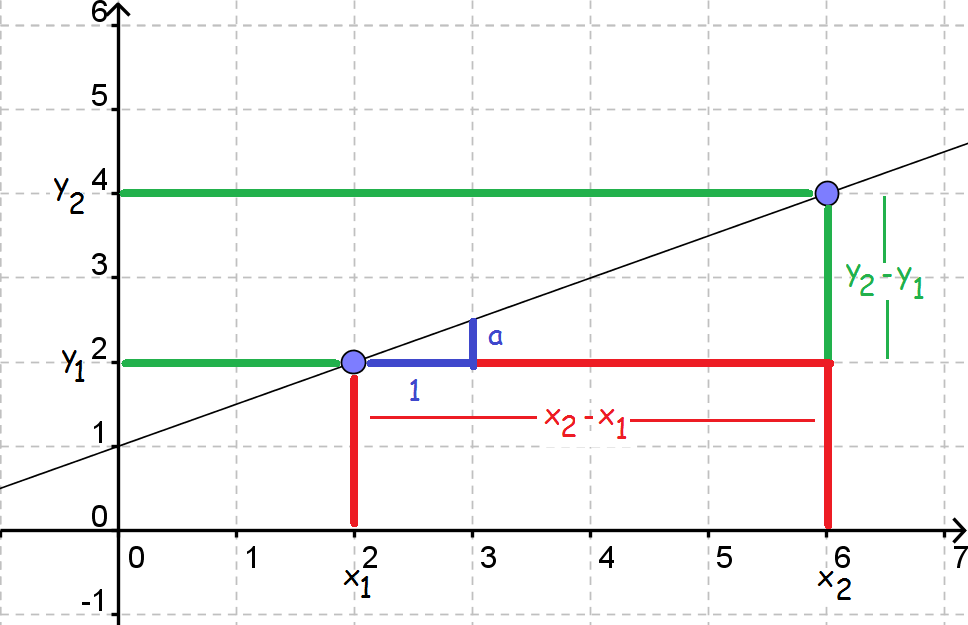
Vi kan på billedet se, at de to trekanter er ensvinklede dvs. at

$$a=k\cdot(y_2-y_1)$$

$$1=k\cdot(x_2-x_1)$$

Hvis vi dividerer den øverste ligning med den nederste, får vi

$$\frac{a}{1}=\frac{k\cdot(y_2-y_1)}{k\cdot(x_2-x_1)}$$

$$a=\frac{\not k\cdot(y_2-y_1)}{\not k\cdot(x_2-x_1)}$$

$$a=\frac{y_2-y_1}{x_2-x_1}$$

Det vil altså sige, at hvis vi kender koordinaterne til to punkter, kan vi beregne a ved hjælp af formlen

$$a=\frac{y_2-y_1}{x_2-x_1}$$

Når vi først har fundet a, kan vi let finde b. Da vores to punkter ligger på grafen, betyder det, at vi kan sætte dem ind på hver sin side af lighedstegnet i den rette linjes ligning.

$$y_1=a\cdot x_1+b$$

$$y_2=a\cdot x_2+b$$

Herefter er det bare at isolere b

$$y_1=a\cdot x_1+b \Leftrightarrow b=y_1-a\cdot x_1$$

$$y_2=a\cdot x_2+b\Leftrightarrow b=y_2-a\cdot x_2$$

Og vi har således to formler for at finde b.

$$b=y_1-a\cdot x_1$$

$$b=y_2-a\cdot x_2$$

Lad os se på et eksempel.

Lad os sige, at vi har punkterne (2, 3) og (4, 7). Dvs x₁=2, y₁=3, x₂=4 og y₂=7.
Vi starter med at finde a

$$a=\frac{y_2-y_1}{x_2-x_1}=\frac{7-3}{4-2}=\frac{4}{2}=2$$

Nu ved vi at a=2, og vi kan finde b ved en hvilken som helst at de to formler ovenfor.

$$b=y_1-a\cdot x_1=3-2\cdot2=3-4=-1$$

$$b=y_2-a\cdot x_2=7-2\cdot4=7-8=-1$$

Altså er a=2 og b= -1. Forskriften for den rette linje vil således være

$$y=2x-1$$

Videolektion