Find a og b (eksponentiel)
Vi vil her gennemgå, hvordan man finder konstanterne a og b (fremskrivningsfaktoren og skæringen med y-aksen) for en eksponentiel funktion, når man kender to punkter på grafen.
Lad os starte med at kalde de to punkter på grafen for hhv.
$$\left ( x_1, \,y_1 \right )\, \text{og}\, \left (x_2,\,y_2 \right )$$
Først finder vi fremskrivningsfaktoren. Den findes ved hjælp af formlen
$$a=\sqrt[x_2-x_1]{\frac{y_2}{y_1}}$$
Når vi kender fremskrivningsfaktoren, finder vi skæringen med y-aksen ved at isolere b i en af de to ligninger:
$$y_1=b\cdot a^{x_1}$$
$$y_2=b\cdot a^{x_2}$$
Dvs
$$b=\frac{y_1}{a^{x_1}}$$
$$b=\frac{y_2}{a^{x_2}}$$
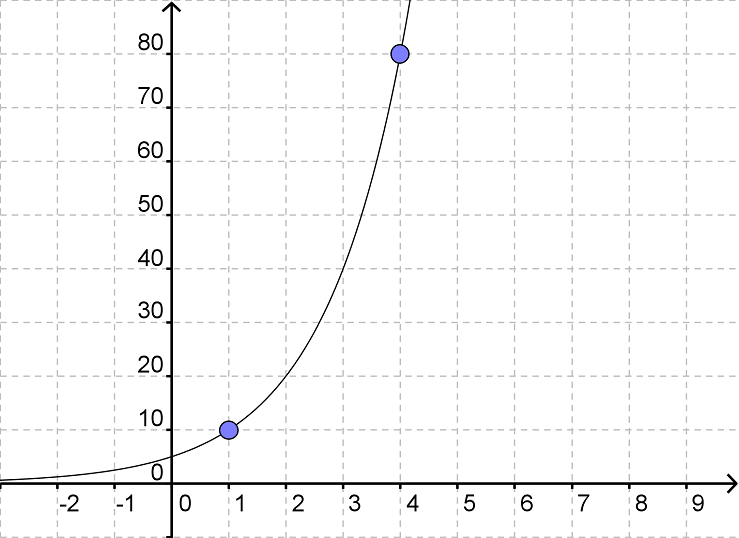
Lad os se på et eksempel. Vi ønsker at bestemme forskriften for den eksponentielle funktion, der går gennem punkterne (1, 10) og (4, 80). Så er x1=1, y1=10, x2=4 og y2=80.
Vi finder først a
$$a=\sqrt[x_2-x_1]{\frac{y_2}{y_1}}=\sqrt[4-1]{\frac{80}{10}}=\sqrt[3]{8}=2$$
Nu kender vi a og kan beregne b. Vi behøver kun bruge en af formlerne for b, men nu viser vi, at man kan bruge begge.
$$b=\frac{y_1}{a^{x_1}}=\frac{10}{2^1}=\frac{10}{2}=5$$
$$b=\frac{y_2}{a^{x_2}}=\frac{80}{2^4}=\frac{80}{16}=\frac{16\cdot5}{16}=\frac{\not16\cdot5}{\not16}=5$$
Altså er forskriften for den eksponentielle funktion
$$y=5\cdot2^x$$