Ensvinklede trekanter
Ensvinklede trekanter spiller en vigtig rolle i teorien for trigonometri, så de er rigtig vigtige at få styr på.
Vi siger, at to trekanter er ensvinklede (eller ligedannede), hvis deres vinkler er parvist lige store.
Ensvinklede trekanter vil have samme form, og den eneste forskel på dem vil være, at den ene er en forstørrelse/formindskelse af den anden.
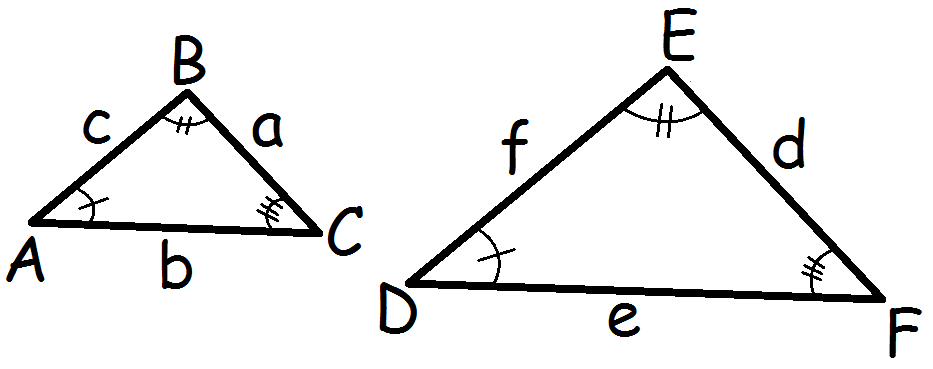
På tegningen kan vi se at
$$\angle A=\angle D$$
$$\angle B=\angle E$$
$$\angle C=\angle F$$
Derfor er de to trekanter ensvinklede.
Hvis man med symboler vil skrive, at de er ensvinklede, skriver man:
$$\triangle ABC \sim \triangle DEF$$
De sider der ligger overfor ens vinkler kaldes ensliggende. F.eks. er a og d ensliggende sider på tegningen herover, fordi de ligger overfor vinklerne A og D, der er lige store. Siderne b og e er også ensliggende, og lige så er c og f.
Som nævnt ovenfor vil ΔDEF være en forstørrelse af ΔABC.
Der findes altså et målestoksforhold mellem de to trekanter. Hvis vi siger, at de er i målestok 1:k, så gælder der at
$$d=k\cdot a$$
$$e=k\cdot b$$
$$f=k\cdot c$$
Dette betyder, at forholdet mellem de ensliggende sider vil være konstant.
$$\frac{d}{a}=\frac{e}{b}=\frac{f}{c}=k$$
Dette er en meget vigtig egenskab ved ensvinklede trekanter, som man blandt meget andet bruger til at forklare cosinus og sinus.
Målestokforholdet betyder også, at forholdet mellem to sider i den samme trekant vil være det samme som forholdet mellem de ensliggende sider i den anden trekant. F.eks.
$$\frac{a}{b}=\frac{k\cdot a}{k\cdot b}=\frac{d}{e}$$
Her forlængede vi brøken med k, hvorefter vi så at \(d=k\cdot a\) og \(e=k\cdot b\).
