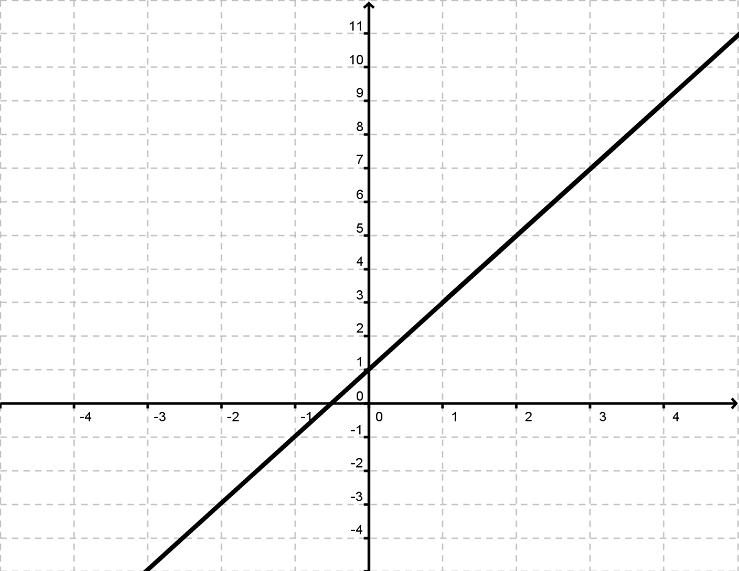
Lineære funktioner
Hvis alle punkter på en graf ligger på en ret linje, siger vi, at funktionen er lineær. Dette kunne f.eks. være funktionen
$$y=x+3$$
Hvis vi kommer forskellige tal ind på x's plads, får vi de tilsvarende y-værdier. Vi kan altså se, at x og y er variable, og at y afhænger af x. Derfor siger vi, at y er en funktion af x. Vi kan skrive de forskellige talpar ind i en tabel, der ofte kaldes et sildeben.
| x | 0 | 1 | 3 | 8 | 10 | 100 |
| y | 3 | 4 | 6 | 11 | 13 | 103 |
Generelt kan vi sige, at en lineær funktion er en funktion, der har forskriften
$$y=ax+b$$
x og y er variable. Men hvad betyder tallene a og b?
Tallet a kaldes hældningskoefficienten, og tallet b kaldes skæringspunktet med y-aksen.
Hældningskoefficienten skal forstås som så meget, vores y-værdi vokser, hver gang vores x-værdi vokser med 1.
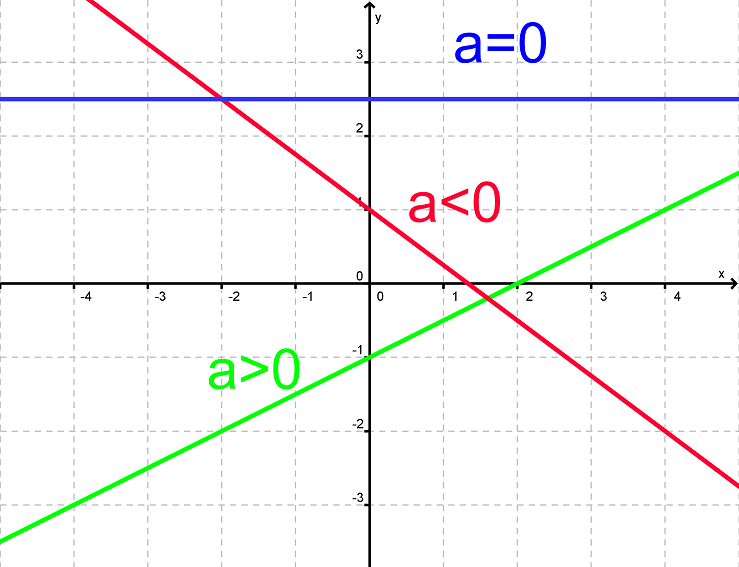
Hvis hældningskoefficienten er positiv vil funktionen altså vokse (så grafen starter nede til venstre og bevæger sig op mod højre), og hvis hældningskoefficienten er negativ, vil funktionen aftage (så grafen starter oppe til venstre og bevæger sig ned mod højre).
Hvis hældningskoefficienten er 0, vil funktionen hverken vokse eller aftage, og grafen vil således være parallel med x-aksen.
Da hældningskoefficienten bestemmes ud fra, hvor meget y vokser for hvert x, er det muligt at aflæse hældningskoefficienten på grafen ved (fra et valgfrit startpunkt) at gå 1 ud på x-aksen og se, hvor meget grafen bevæger sig opad.
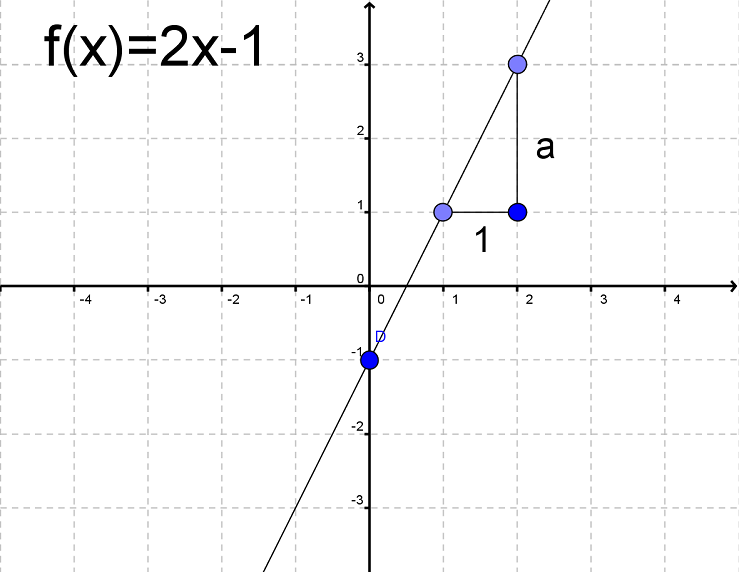
På grafen ovenfor kan vi se, at man går 2 op, hver gang man bevæger sig 1 hen ad x-aksen. Derfor er a=2.
b er en konstant, der afgør, hvor grafen skærer y-aksen. Hvis b er positiv finder skæringen sted ovenfor origo, og hvis b er negativ er skæringen placeret under origo. Hvis b=0, skærer grafen yaksen i origo. I dette tilfælde skriver man funktionen som y=ax, og vi kalder det for ligefrem proportionalitet.
På billedet ovenfor kan vi aflæse b ved at se hvor grafen skærer y-aksen. Denne skæring er i punktet (0, -1). Derfor er b= -1
Grafen
Alle lineære funktioner har grafer, der er rette linjer. Man kan tegne grafen ud fra 2 punkter. Hvis vi f.eks. gerne vil tegne grafen for y=2x+1, så starter vi med at lave et sildeben
| x | 1 | 2 | 3 | 4 |
| y | 3 | 5 | 7 | 9 |
Vi udvælger to punkter, det kunne være det første og det sidste, og tegner dem ind i et koordinatsystem.
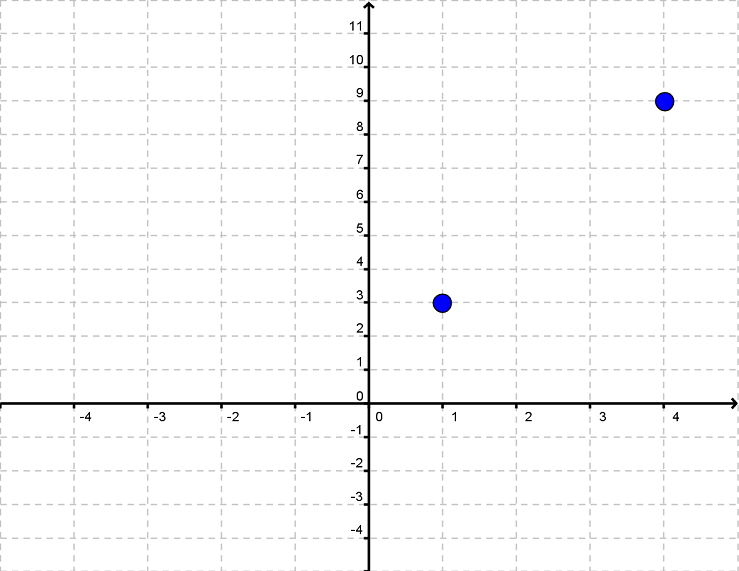
Nu kan vi tegne en ret linje mellem de to punkter
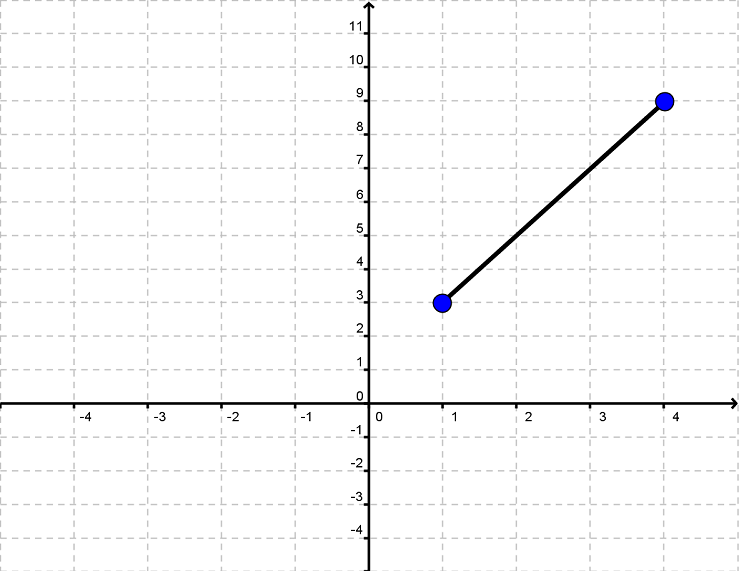
Vi kan se, at de øvrige punkter fra sildebenet (2, 5) og (3, 7) også ligger på denne linje.
Til sidst kan vi fortsætte linjen ud til både højre og venstre for at få grafen for y=2x+1