Spejling

Hvis man har en figur og en linje, så kan man spejle figuren i linjen. Det gør man ved fra hvert punkt i figuren at gå vinkelret ind på spejlingslinjen og fortsætte lige så langt på den anden side af linjen.

Hvis der er tale om en trekant, en firkant, en femkant eller en anden polygon, så er det nok at spejle hjørnerne og så forbinde dem på den anden side af spejlingslinjen.

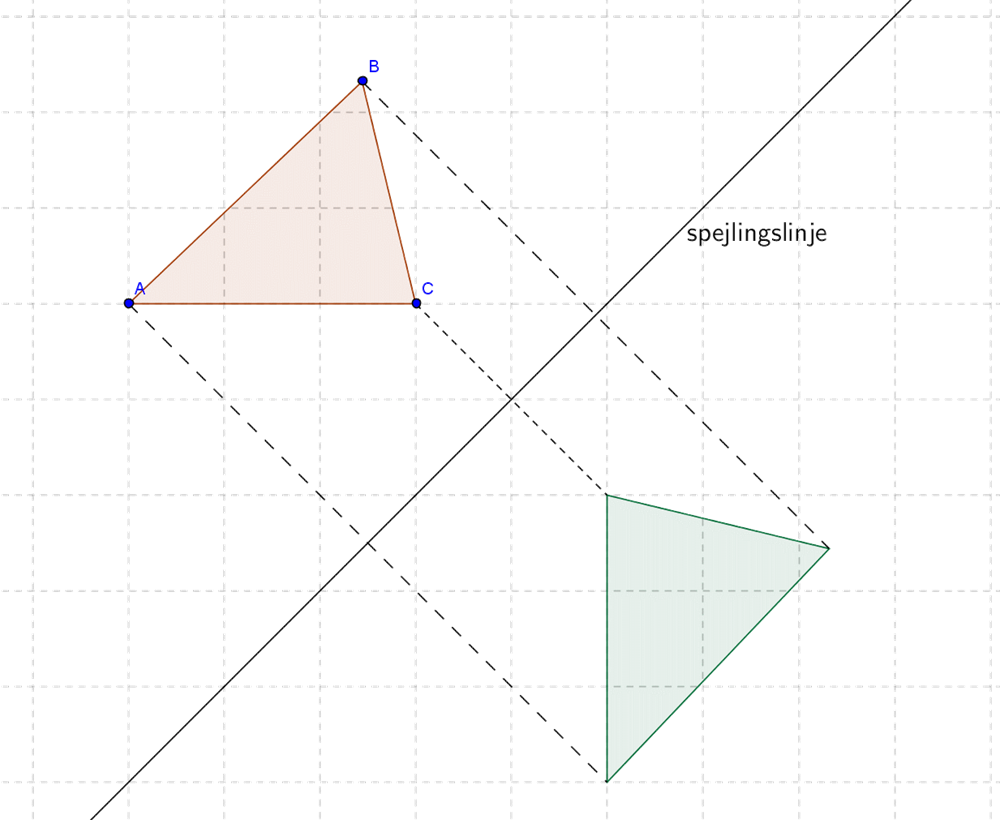
På figuren herover er trekanten \(\triangle ABC\) spejlet i linjen.

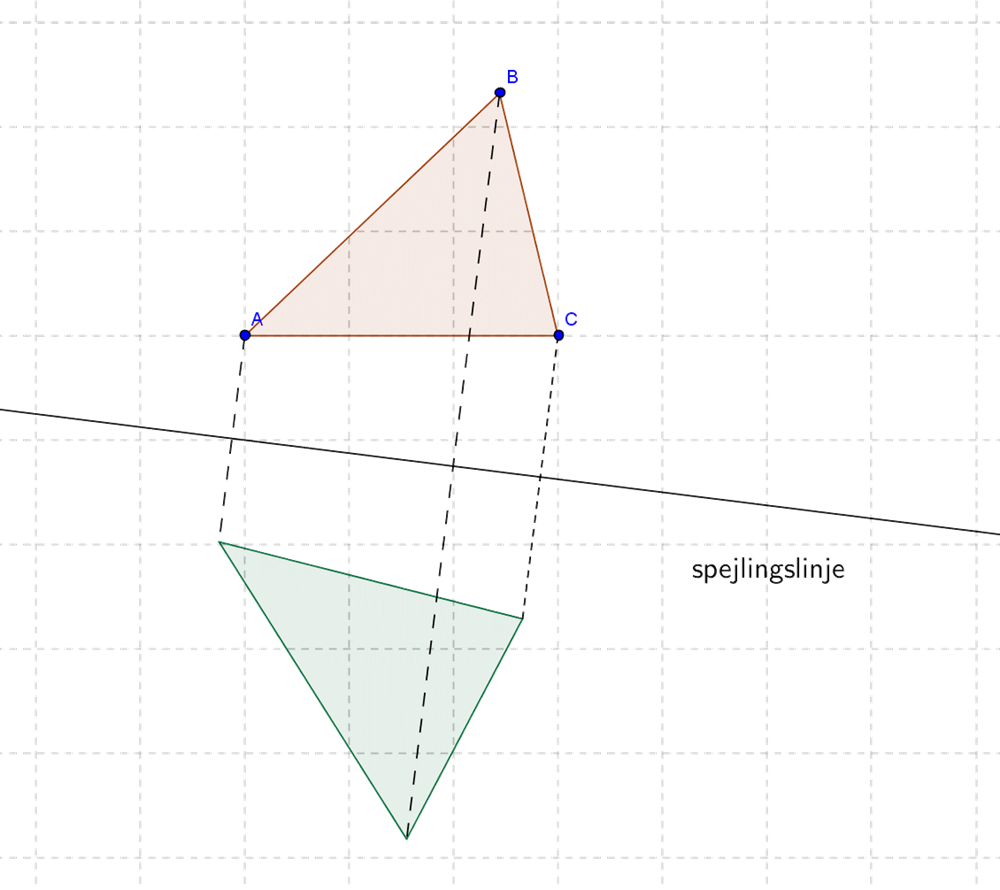
Herunder er den samme trekant spejlet i en anden linje

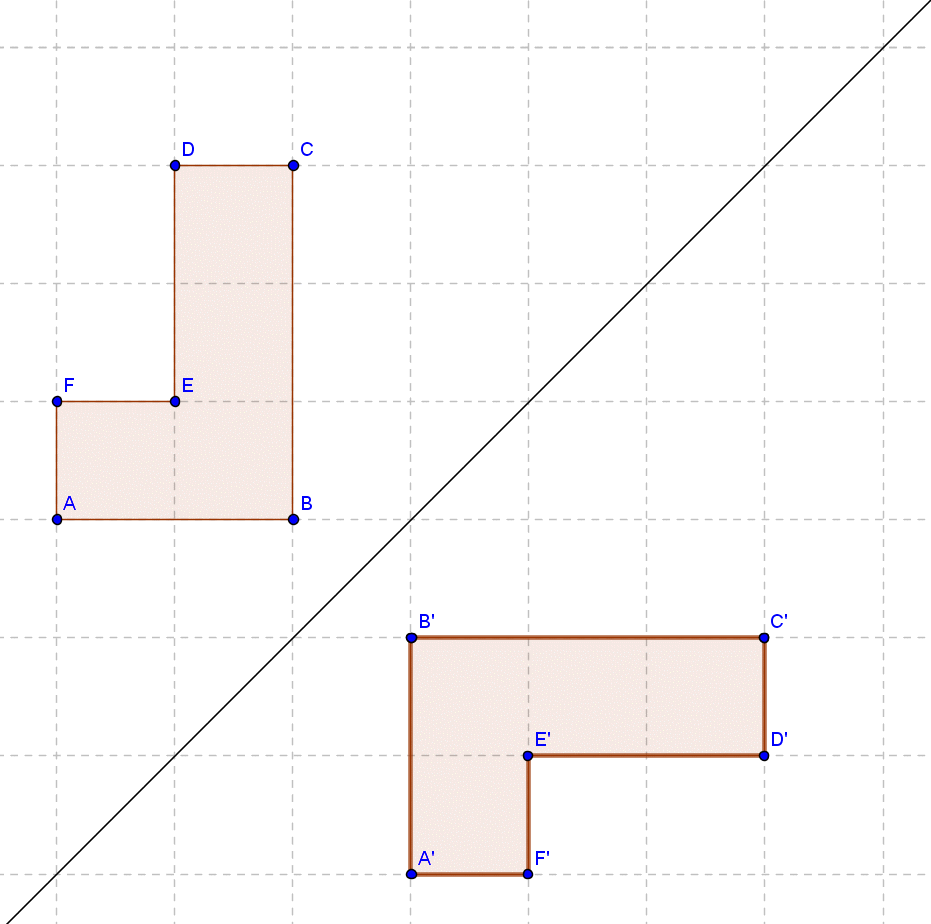
Spejling i koordinatsystem

Når man skal spejle en figur, er det en god ide at have et koordinatsystem, da det gør det lettere at se, om man spejler de rigtige steder hen.

Det er især en fordel, hvis spejlingslinjen er parallel med en af akserne (lodret eller vandret) eller hælder 45 grader (som i eksemplet herunder).

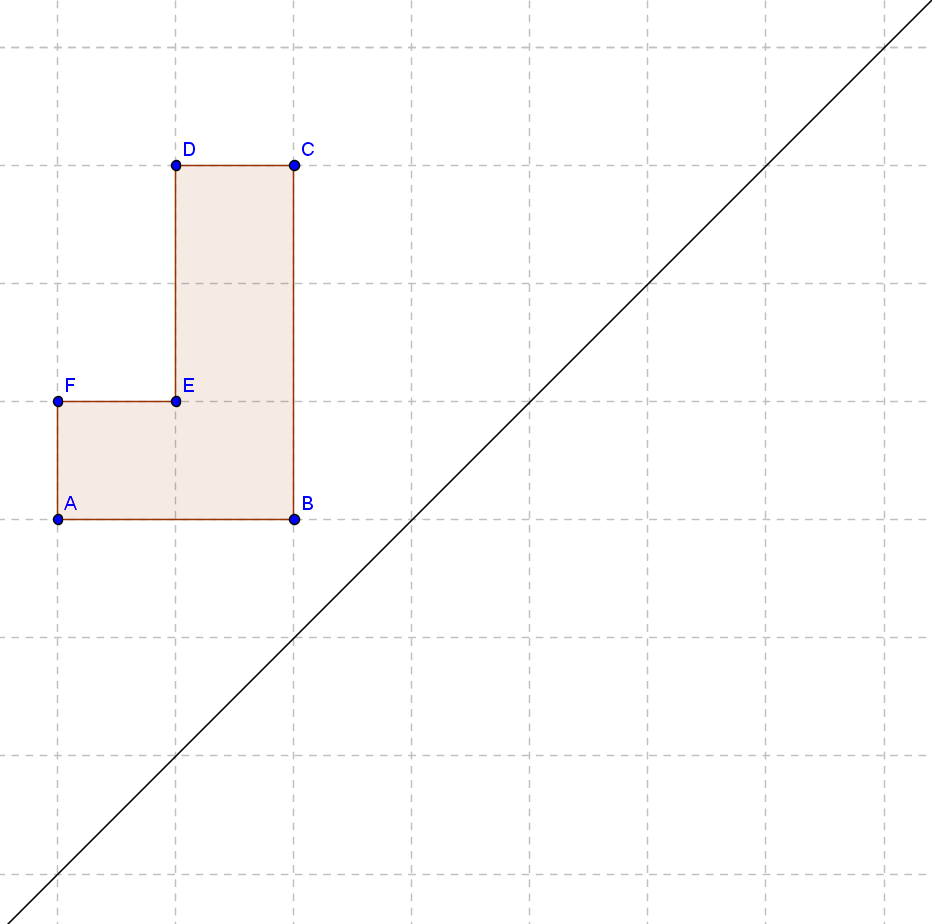
Fra hvert punkt går man vinkelret ind på spejlingslinjen og lige så langt ud igen på den anden side. Når man har ternene til hjælp er det let at se, hvor langt man skal gå.

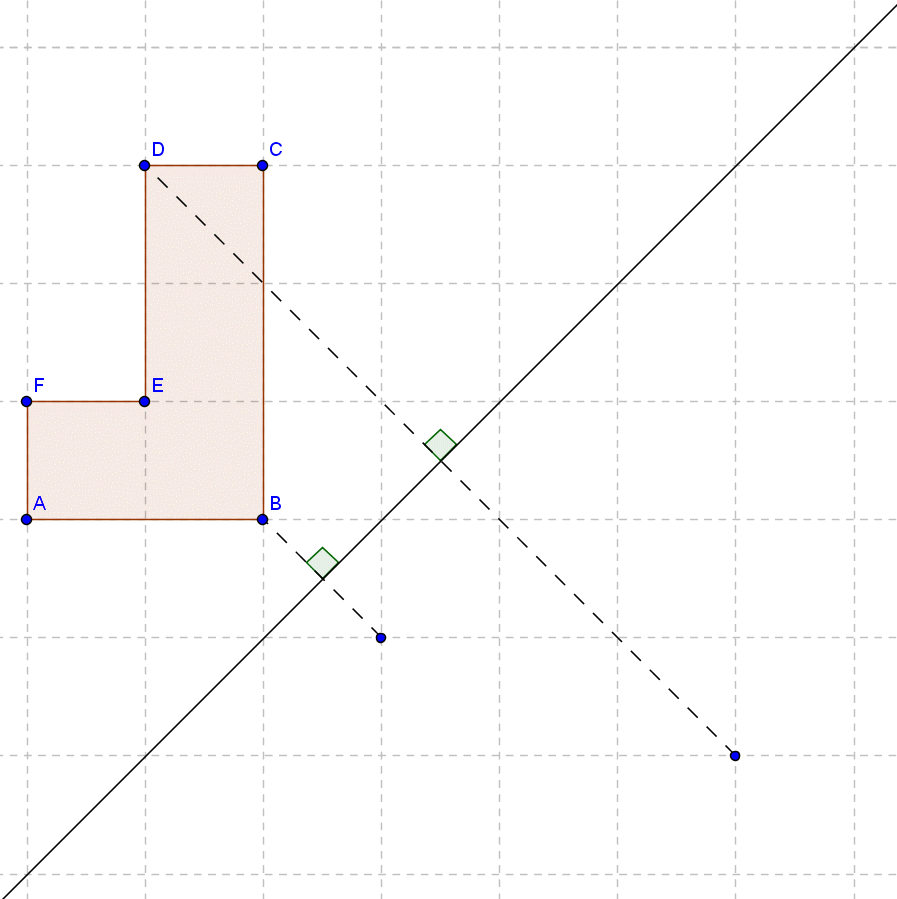
Når man har spejlet alle punkterne over, forbinder man dem, og vupti, har man en spejling.