Brøkers størrelse

Nogle gange kan det være svært at sammenligne brøkers størrelse. Er \(\frac{3}{10}\) f.eks. større end eller mindre end \(\frac{2}{7}\)?

Generelt kan man sige, at hvis tælleren ikke ændrer sig, så gælder det at jo større nævneren (tallet under brøkstregen) bliver, des mindre bliver brøken. F.eks. er \(\frac{1}{100}\) (en hundrededel) mindre end \(\frac{1}{10}\) (en tiendedel).

Det kan virke mærkeligt, da 100 jo er større end 10. Man kan tænke på det som en stor bradepandekage. Hvis der er 100, der gerne vil smage kagen, så bliver stykkerne meget små (hver af dem bliver \(\frac{1}{100}\) af kagen), mens hvis der kun er 10, der vil have kage, så bliver hvert stykke større (hvert stykke bliver \(\frac{1}{10}\) af kagen).

Fællesnævner, forlænge og forkorte brøker

Hvis man vil sammenligne to brøker, er det lettest, hvis de har den samme nævner.

Det svarer nemlig til, at man har skåret kagerne ud i lige store stykker, og så sammenligner, hvor mange stykker hver har fået.

For at nå frem til en fællesnævner skal man huske på, at man må gange med det samme tal i både tæller og nævner af en brøk, uden at den ændrer værdi. Det kaldes at forlænge brøken. F.eks. er

$$\frac{3}{4}=\frac{5\cdot3}{5\cdot4}=\frac{15}{20}.$$

Her har vi forlænget brøken \(\frac{3}{4}\) med 5.

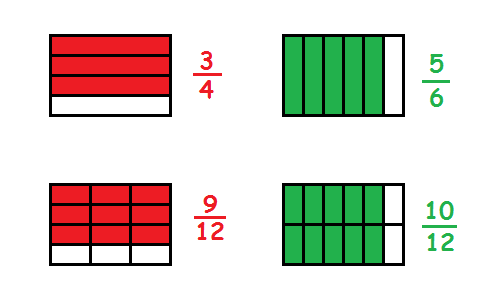
Man kan f.eks. ønske at finde ud af, hvad der er størst af \(\frac{5}{6}\) og \(\frac{3}{4}\). Vi skal først forlænge brøkerne, så vi får den samme nævner. Vi skal altså finde et tal, som begge nævnere (6 og 4) går op i. F.eks. kunne vi vælge 12 som fællesnævner. Så skal vi forlænge den første brøk med 2 for at få den omskrevet til tolvtedele, mens vi skal forlænge den anden brøk med 3 for at få den omskrevet til tolvtedele

$$\frac{5}{6}=\frac{2\cdot5}{2\cdot6}=\frac{10}{12},$$

$$\frac{3}{4}=\frac{3\cdot3}{3\cdot4}=\frac{9}{12}.$$

Da \(\frac{10}{12}\) er større end \(\frac{9}{12}\) er \(\frac{5}{6}\) større end \(\frac{3}{4}\).

Hvis man af den ene eller anden grund ikke kan finde et tal som begge nævnere går op i, så kan man altid tage den sikre udvej, og forlænge med nævneren fra den ene brøk i den anden brøk, og omvendt. Hvis vi tager udgangspunkt i brøkerne ovenfor ønsker vi først at forlænge \(\frac{3}{4}\) med 6 (nævneren fra den anden brøk)

$$
\frac{3}{4} = \frac{3\cdot6}{4\cdot6} = \frac{18}{24},
$$

samt at forlænge \(\frac{5}{6}\) med 4

$$
\frac{5}{6} = \frac{5\cdot4}{6\cdot4} = \frac{20}{24}.
$$

Igen når vi frem til at \(\frac{5}{6}\) er større end \(\frac{3}{4}\).