Trekanter

Enhver trekant har naturligvis tre sider og tre hjørner. Der gælder for alle trekanter at summen af de tre vinkler i enhver trekant er \(180^{\circ}\). Da der kun er tre vinkler i hver trekant kan vi karakterisere forskellige trekanter ud fra disse på følgende måde:

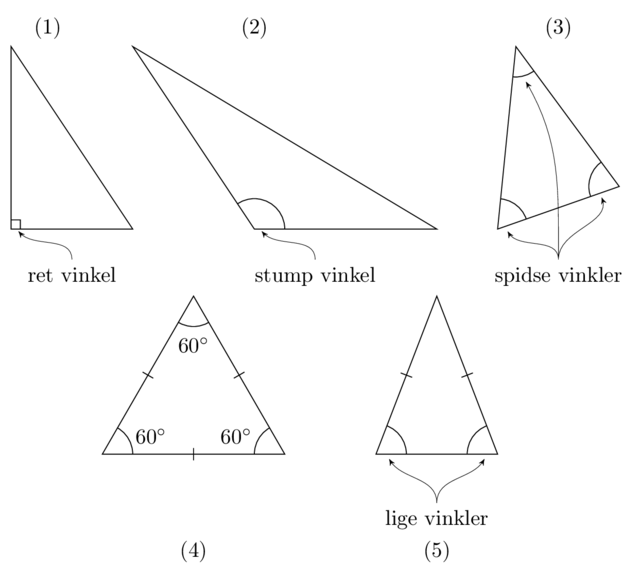
1. En retvinklet trekant har en ret vinkel, altså en vinkel som er \(90^{\circ}\). Der kan kun være én ret vinkel i en trekant, da vinkelsummen af to rette vinkler er \(180^{\circ}\), hvilket ville betyde at den sidste vinkel skulle være \(0^{\circ}\) og så er det jo ikke en trekant.
2. En stumpvinklet trekant har en stump vinkel, det vil sige en vinkel som er over \(90^{\circ}\). Ligesom før kan vi kun have én stump vinkel i en trekant, da vinkelsummen ellers ville være større end \(180^{\circ}\).
3. En spidsvinklet trekant har hverken en stump eller ret vinkel, og dermed er alle vinklerne i trekanten spidse, altså mindre end \(90^{\circ}\).
4. I en ligesidet trekant er alle sider lige lange hvilket medfører at alle vinkler også skal være lige store. Dermed er hver af vinklerne \(\frac{1}{3}\cdot 180^{\circ}=60^{\circ}\).
5. I en ligebenet trekant er 2 af siderne lige lange, og dermed er også 2 af vinklerne lige store, og spidse. I nogle definitioner hører ligesidede trekanter under ligebenede, i andre definitioner kræves det, at netop to sider er lige lange.

Før vi går videre med disse trekanter skal vi have lidt terminologi på plads.

Midtnormal, vinkelhalveringslinje og median

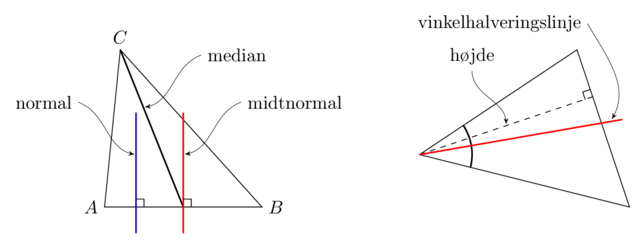
En normal linje er en linje der tegnes vinkelret på en anden linje. Hvis vi tager en af trekantens sider så vil midtnormalen være den linje der tegnes vinkelret midt på trekantens side (se billedet til venstre). 

Medianen er en linje som forbinder et hjørne med midtpunktet af siden der ligger overfor (se billedet til venstre).

Vinkelhalveringslinjen  er en linje der går gennem en vinkel og halverer den (se billedet til højre).

Ligebenede og ligesiddede trekanter

For ligesiddede trekanter gælder der altid at medianen, midtnormalen, vinkelhalveringslinjen og højden er den samme linje (se figuren nedenunder).

For ligebenede trekanter gælder det samme, men kun hvis den tegnes fra den vinkel som ikke er lige  (dvs. hvis de tegnes fra toppen af den ligebenede trekant i figuren ovenfor eller se figuren nedenunder)!

Omskreven cirkel 

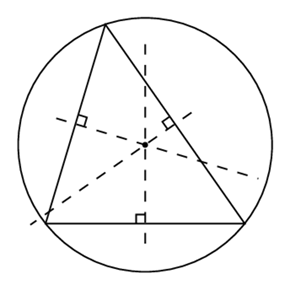
En omskreven cirkel er en cirkel som ligger udenfor en figur, men som har ét berøringspunkt med hvert hjørne af figuren. Alle trekanter og kvadrater (men ikke vilkårlige firkanter) har en omskreven cirkel.

Der findes en sammenhæng mellem en omskreven cirkel og midtnormalerne i en trekant. Det er nemlig sådan at skæringspunktet for midtnormalerne netop sker i centrum af den omskrevne cirkel.

Indskreven cirkel

En indskreven cirkel er en cirkel som kan tegnes inde i en figur på en sådan måde at cirklen har ét (og kun ét!) berøringspunkt med hver side af figuren.

Der findes også en sammenhæng mellem den indskrevne cirkel og vinkelhalveringslinjerne. Det er nemlig, som i tilfældet med den omskrevne cirkel, at skæringspunktet for vinkelhalveringslinjerne netop sker i centrum af den indskrevne cirkel.