Regneregler for brøker
I følgende afsnit vil vi se på hvordan vi
- lægger to brøker sammen,
- trækker to brøker fra hinanden,
- ganger to brøker sammen (eller ganger en brøk med et tal), og
- dividerer brøker med hinanden.
Lægge brøker sammen
Når man skal lægge brøker sammen eller trække dem fra hinanden, så er det vigtigt, at de har den samme nævner. Man siger, at de skal have fællesnævner.
Det er klart, fordi ét stykke af en kage, der er skåret i 10 stykker, ikke repræsenterer lige så meget kage som ét stykke af en kage af samme størrelse, der er skåret i 6 stykker. Man er nødt til at sørge for at stykkerne er lige store, før man begynder at lægge dem sammen eller trække dem fra hinanden (se evt. forrige afsnit om brøkers størrelse).
Vi ønsker at udregne
$$\frac{2}{3}+\frac{1}{4}=\;?$$
Først finder en fællesnævner for brøken. I dette tilfælde vælger vi fællesnævneren til 12 da både 3 og 4 går op i 12. Vi forlænger \(\frac{2}{3}\) med 4 og \(\frac{1}{4}\) med 3
$$\frac{2}{3}=\frac{4\cdot2}{4\cdot3}=\frac{8}{12},$$
$$\frac{1}{4}=\frac{3\cdot1}{3\cdot4}=\frac{3}{12}.$$
Nu har brøkerne samme nævner, og vi kan derfor lægge dem sammen. Det gør man ved at lægge tællerne (tallene over brøkstregerne) sammen.
$$\frac{2}{3}+\frac{1}{4}=\frac{8}{12}+\frac{3}{12}=\frac{8+3}{12}=\frac{11}{12}.$$
Man kan illustrere udregningen med et billede.
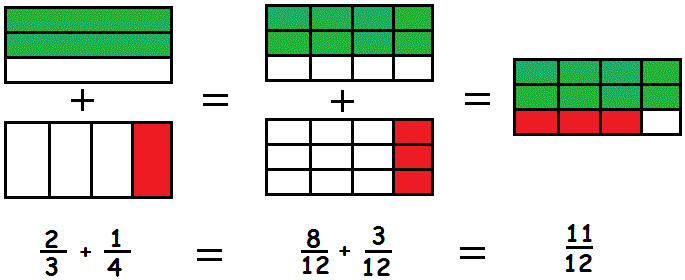
Trække brøker fra hinanden
Når man skal trække en brøk fra en anden brøk, så skal man også sikre sig, at de har samme nævner. Derefter trækker man den ene tæller fra den anden. Lad os se på et eksempel.
Vi vil udregne
$$\frac{4}{7}-\frac{3}{14}=\;?$$
Et tal som både 7 og 14 går op i er 14. Brøken \(\frac{3}{14}\) står allerede i fjortendedele, så den lader vi være. Brøken \(\frac{4}{7}\) skal vi forlænge med 2 for at få den omskrevet til fjortendedele.
$$\frac{4}{7}=\frac{2\cdot4}{2\cdot7}=\frac{8}{14}.$$
Nu er begge brøker i fjortendedele, og vi kan trække den ene fra den anden.
$$\frac{4}{7}-\frac{3}{14}=\frac{8}{14}-\frac{3}{14}=\frac{8-3}{14}=\frac{5}{14}.$$
Generelt kan reglerne skrives op sådan her
$$\frac{a}{b}+\frac{c}{b}=\frac{a+c}{b},$$
$$\frac{a}{b}-\frac{c}{b}=\frac{a-c}{b}.$$
Gange brøker sammen
Når man skal gange to brøker med hinanden, skal man bare gange tæller med tæller og nævner med nævner.
Man behøver altså ikke at finde fællesnævnere og al den slags, som vi gjorde da vi skulle lægge dem sammen eller trække dem fra hinanden.
F.eks. er
$$\frac{4}{5}\cdot\frac{2}{7}=\frac{4\cdot2}{5\cdot7}=\frac{8}{35}.$$
Hvis man skal gange et helt tal med en brøk, så ganger man det på i tælleren.
F.eks.
$$3\cdot\frac{2}{7}=\frac{3\cdot2}{7}=\frac{6}{7}.$$
Generelt kan reglerne skrives op med symboler sådan her:
$$\frac{a}{b}\cdot\frac{c}{d}=\frac{a\cdot c}{b\cdot d},$$
$$\frac{a}{b}\cdot c=\frac{a\cdot c}{b},$$
$$c\cdot\frac{a}{b}=\frac{a\cdot c}{b}.$$
Division med brøker
Når det kommer til division og brøker er der tre muligheder
- vi deler to brøker med hinanden,
- vi deler en brøk med et tal,
- vi deler et tal med en brøk.
Disse tre scenarier vil vi nu kigge på!
Dividere brøk med brøk
Når man skal dividere en brøk med en anden brøk, så svarer det til at ”vende den bagerste brøk på hovedet” og derefter gange de to brøker med hinanden.
F.eks. er
$$\frac{1}{5}:{\color{Red} {\frac{3}{4}}} = \frac{1}{5}\cdot{\color{Red} {\frac{4}{3}}}\begin{matrix}\nwarrow\\\swarrow \end{matrix}\mathrm{byt} \ \mathrm{om} = \frac{4}{15}.$$
Det er vigtigt, at det er den brøk, man dividerer med, som man vender om!
Generelt er reglen
$$\frac{a}{b}:\frac{c}{d}=\frac{a}{b}\cdot\frac{d}{c}\begin{matrix}\nwarrow\\\swarrow \end{matrix}\mathrm{byt} \ \mathrm{om}.$$
Dividere brøk med tal
Når man skal dividere et brøk med et tal, så ganger man tallet på i nævneren. F.eks er
$$\frac{5}{6}:2 = \frac{5}{6\cdot2} = \frac{5}{12}.$$
En måde at huske denne regel på er ved at omskrive tallet til en brøk. (Ethvert tal svarer nemlig til en brøk med 1 i nævneren). Nu er den hen regel egentlig bare den samme som division af brøk med brøk. Eksemplet ovenfor ville blive
$$\frac{5}{6}:2 = \frac{5}{6}:{\color{Red} {\frac{2}{1}}} = \frac{5}{6}\cdot{\color{Red} {\frac{1}{2}}} = \frac{5\cdot1}{6\cdot2} = \frac{5}{12}.$$
Dividere tal med brøk
Når man skal dividere et tal med en brøk, så vender man brøken om og ganger tallet på i (den nye) tæller.
F.eks. er
$$8:{\color{Red} {\frac{19}{2}}} = 8\cdot {\color{Red} {\frac{2}{19}}} = \frac{8\cdot2}{19} = \frac{16}{19}.$$
Igen kan vi omskrive tallet til en brøk med 1 i nævneren, og så er også denne regel den samme som division af brøk med brøk.
$$8:\frac{19}{2} = \frac{8}{1} : {\color{Red}{\frac{19}{2}}} = \frac{8}{1}\cdot {\color{Red} {\frac{2}{19}}} = \frac{8\cdot2}{1\cdot19} = \underline{\underline{\frac{16}{19}}}.$$
